
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() ,
,![]() ,
,![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)若![]() .①当
.①当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
②证明![]() 是定值,并求出此定值.
是定值,并求出此定值.
科目:高中数学 来源: 题型:
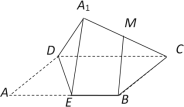
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() 为边
为边![]() 的中点.将
的中点.将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() (点
(点![]() 不落在底面
不落在底面![]() 内).若
内).若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻转过程中,以下命题正确的是( )
翻转过程中,以下命题正确的是( )
A.四棱锥![]() 体积最大值为
体积最大值为![]()
B.线段![]() 长度是定值;
长度是定值;
C.![]() 平面
平面![]() 一定成立;
一定成立;
D.存在某个位置,使![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
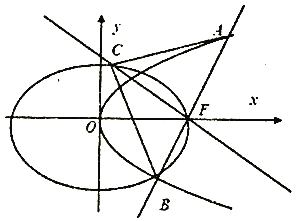
【题目】如图,设椭圆![]() :
: ![]() ,长轴的右端点与抛物线
,长轴的右端点与抛物线![]() :
: ![]() 的焦点
的焦点![]() 重合,且椭圆
重合,且椭圆![]() 的离心率是
的离心率是![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点,过
两点,过![]() 且与直线
且与直线![]() 垂直的直线交椭圆
垂直的直线交椭圆![]() 于另一点
于另一点![]() ,求
,求![]() 面积的最小值,以及取到最小值时直线
面积的最小值,以及取到最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]()
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,当
两点,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年央视大型文化节目《经典咏流传》的热播,在全民中掀起了诵读诗词的热潮,节目组为热心观众给以奖励,要从
年央视大型文化节目《经典咏流传》的热播,在全民中掀起了诵读诗词的热潮,节目组为热心观众给以奖励,要从![]() 名观众中抽取
名观众中抽取![]() 名幸运观众.先用简单随机抽样从
名幸运观众.先用简单随机抽样从![]() 人中剔除
人中剔除![]() 人,剩下的
人,剩下的![]() 人再按系统抽样方法抽取
人再按系统抽样方法抽取![]() 人,则在
人,则在![]() 人中,每个人被抽取的可能性( )
人中,每个人被抽取的可能性( )
A. 均不相等B. 都相等,且为![]()
C. 不全相等D. 都相等,且为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,且椭圆C上恰有三点在集合
,且椭圆C上恰有三点在集合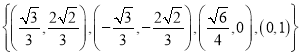 中.
中.
(1)求椭圆C的方程;
(2)若点O为坐标原点,直线AB与椭圆交于A、B两点,且满足![]() ,试探究:点O到直线AB的距离是否为定值.如果是,请求出定值:如果不是,请明说理由.
,试探究:点O到直线AB的距离是否为定值.如果是,请求出定值:如果不是,请明说理由.
(3)在(2)的条件下,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一场专家报告会,张老师带甲,乙,丙,丁四位同学参加,其中有一个特殊位置可与专家近距离交流,张老师看出每个同学都想去坐这个位置,因此给出一个问题,谁能猜对,谁去坐这个位置.问题如下:某班10位同学参加一次全年级的高二数学竞赛,最后一道题只有6名同学![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 尝试做了,并且这6人中只有1人答对了.听完后,四个同学给出猜测如下:甲猜:
尝试做了,并且这6人中只有1人答对了.听完后,四个同学给出猜测如下:甲猜:![]() 或
或![]() 答对了;乙猜:
答对了;乙猜:![]() 不可能答对;丙猜:
不可能答对;丙猜:![]() ,
,![]() ,
,![]() 当中必有1人答对了;丁猜:
当中必有1人答对了;丁猜:![]() ,
,![]() ,
,![]() 都不可能答对,在他们回答完后,张老师说四人中只有1人猜对,则张老师把特殊位置给了__________.
都不可能答对,在他们回答完后,张老师说四人中只有1人猜对,则张老师把特殊位置给了__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是双曲线
是双曲线![]() :
:![]() 的右焦点,
的右焦点,![]() 是
是![]() 左支上的点,已知
左支上的点,已知![]() ,则
,则![]() 周长的最小值是_______.
周长的最小值是_______.
【答案】![]()
【解析】
设左焦点为![]() ,利用双曲线的定义,
,利用双曲线的定义,![]() 得到当
得到当![]() 三点共线时,三角形
三点共线时,三角形![]() 的周长取得最小值,并求得最小的周长.
的周长取得最小值,并求得最小的周长.
设左焦点为![]() ,根据双曲线的定义可知
,根据双曲线的定义可知![]() ,所以三角形
,所以三角形![]() 的周长为
的周长为![]() ,当
,当![]() 三点共线时,
三点共线时,![]() 取得最小值,三角形
取得最小值,三角形![]() 的周长取得最小值.
的周长取得最小值. ![]() ,故三角形周长的最小值为
,故三角形周长的最小值为![]() .
.
【点睛】
本小题主要考查双曲线的定义,考查三角形周长最小值的求法,属于中档题.
【题型】填空题
【结束】
16
【题目】已知![]() 分别是双曲线
分别是双曲线![]() 的左、右焦点,过点
的左、右焦点,过点![]() 作垂直与
作垂直与![]() 轴的直线交双曲线于
轴的直线交双曲线于![]() ,
,![]() 两点,若
两点,若![]() 为锐角三角形,则双曲线的离心率的取值范围是_______.
为锐角三角形,则双曲线的离心率的取值范围是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() 个数
个数![]() 的“倒均值”
的“倒均值”![]() .
.
(1)若数列![]() 的前
的前![]() 项,
项,![]() 的“倒均值”
的“倒均值”![]() . 求
. 求![]() 的通项公式
的通项公式
(2)在(1)的条件下,令![]() ,试研究数列
,试研究数列![]() 的单调性,并给出证明.
的单调性,并给出证明.
(3)在(2)的条件下,设函数![]() ,对于数列
,对于数列![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,
时,![]() 对任意
对任意![]() 恒成立?若存在,求出在最小的实数
恒成立?若存在,求出在最小的实数![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com