
给出下列五个命题中,其中所有正确命题的序号是_______.
①函数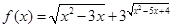 的最小值是3
的最小值是3
②函数 若
若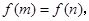 且
且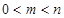 ,则动点
,则动点 到直线
到直线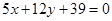 的
的
最小距离是 .
.
③命题“函数 当
当
 ”是真命题.
”是真命题.
④函数 的最小正周期是1的充要条件是
的最小正周期是1的充要条件是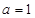 .
.
⑤已知等差数列 的前
的前 项和为
项和为 ,
, 为不共线的向量,又
为不共线的向量,又
若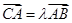 ,则
,则 .
.
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
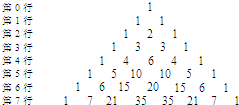 杨辉是中国南宋末年的一位杰出的数学家、数学教育家,他的数学研究与教育工作的重点是在计算技术方面,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关.图是一个7阶的杨辉三角.
杨辉是中国南宋末年的一位杰出的数学家、数学教育家,他的数学研究与教育工作的重点是在计算技术方面,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关.图是一个7阶的杨辉三角.| (n+1)2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| S10 |
| 10 |
| S100 |
| 100 |
| S110 |
| 110 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| AB |
| 3 |
| AC |
| AD |
| AB |
| AC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com