
【题目】已知点H(0,﹣8),点P在x轴上,动点F满足PF⊥PH,且PF与y轴交于点Q,Q为线段PF的中点.
(1)求动点F的轨迹E的方程;
(2)点D是直线l:x﹣y﹣2=0上任意一点,过点D作E的两条切线,切点分别为A、B,取线段AB的中点,连接DM交曲线E于点N,求证:直线AB过定点,并求出定点的坐标.
【答案】
(1)解:设F(x,y),∵Q是PF的中点,Q在y轴上,P在x轴上,
∴P(﹣x,0),又H(0,﹣8),∴kPF= ![]() ,kPH=
,kPH= ![]() ,
,
∵PF⊥PH,∴ ![]() ,即x2=4y.
,即x2=4y.
∴动点F的轨迹E的方程x2=4y
(2)解:证明:设直线AB的方程为y=kx+b,
联立方程组 ![]() ,消去y得:x2﹣4kx﹣4b=0,
,消去y得:x2﹣4kx﹣4b=0,
设A(x1,y1),B(x2,y2),则 ![]() ,且△=16k2+16b.
,且△=16k2+16b.
以点A为切点的切线的斜率为kP= ![]() x1,其切线方程为y﹣y1=
x1,其切线方程为y﹣y1= ![]() x1(x﹣x1),
x1(x﹣x1),
即y= ![]() x1x﹣
x1x﹣ ![]() x12,
x12,
同理过点Q的切线的方程为y= ![]() x2x﹣
x2x﹣ ![]() x22,
x22,
联立方程组 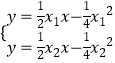 得
得 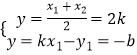 ,
,
即D(2k,﹣b),∵D在直线x﹣y﹣2=0上,
∴2k﹣(﹣b)﹣2=0,即b=2﹣2k,
所以直线AB的方程y=kx+2﹣2k,即y=k(x﹣2)+2,显然该直线恒过定点(2,2).
【解析】(1)设F(x,y),用x,y表示出P点坐标,求出PF、PH的斜率,根据PF⊥PH列方程化简即可;(2)设AB方程为y=kx+b,联立方程组得出A,B坐标的关系,利用导数的几何意义得出切线方程,从而求得D点坐标,得出k,b的关系,即可得出结论.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).则分数在[70,80)内的人数是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2lnx﹣ ![]() ﹣m,若关于x的方程f(f(x))=x恰有两个不相等的实数根,则m的取值范围是( )
﹣m,若关于x的方程f(f(x))=x恰有两个不相等的实数根,则m的取值范围是( )
A.(2ln3﹣4,+∞)
B.(﹣∞,2ln3﹣4)
C.(﹣4,+∞)
D.(﹣∞,﹣4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2.5cos(ωx+φ)(ω>0,|φ|< ![]() )的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( )
)的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( ) 
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 已知a2=7,a3为整数,且Sn的最大值为S5 .
(1)求{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iphone手机的年固定成本为40万美元,每生产1只还需另投入16美元.设苹果公司一年内共生产该款iphone手机x万只并全部销售完,每万只的销售收入为R(x)万美元,且R(x)= 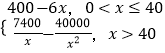
(1)写出年利润W(万元)关于年产量x(万只)的函数解析式;
(2)当年产量为多少万只时,苹果公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
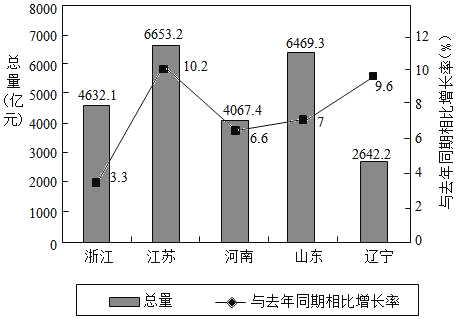
A. 2017年第一季度![]() 总量和增速由高到低排位均居同一位的省只有1个
总量和增速由高到低排位均居同一位的省只有1个
B. 与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长
总量均实现了增长
C. 去年同期河南省的![]() 总量不超过4000亿元
总量不超过4000亿元
D. 2017年第一季度![]() 增速由高到低排位第5的是浙江省
增速由高到低排位第5的是浙江省
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,直线
,直线![]() .
.
(1)求与圆![]() 相切,且与直线
相切,且与直线![]() 垂直的直线方程;
垂直的直线方程;
(2)在直线![]() 上(
上(![]() 为坐标原点),存在定点
为坐标原点),存在定点![]() (不同于点
(不同于点![]() ),满足:对于圆
),满足:对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:
(1)设所求直线方程为![]() ,利用圆心到直线的距离等于半径可得关于b的方程,解方程可得
,利用圆心到直线的距离等于半径可得关于b的方程,解方程可得![]() ,则所求直线方程为
,则所求直线方程为![]()
(2)方法1:假设存在这样的点![]() ,由题意可得
,由题意可得![]() ,则
,则![]() ,然后证明
,然后证明![]() 为常数
为常数![]() 为即可.
为即可.
方法2:假设存在这样的点![]() ,使得
,使得![]() 为常数
为常数![]() ,则
,则![]() ,据此得到关于
,据此得到关于![]() 的方程组,求解方程组可得存在点
的方程组,求解方程组可得存在点![]() 对于圆
对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为常数
为常数![]() .
.
试题解析:
(1)设所求直线方程为![]() ,即
,即![]() ,
,
∵直线与圆相切,∴![]() ,得
,得![]() ,
,
∴所求直线方程为![]()
(2)方法1:假设存在这样的点![]() ,
,
当![]() 为圆
为圆![]() 与
与![]() 轴左交点
轴左交点![]() 时,
时,![]() ;
;
当![]() 为圆
为圆![]() 与
与![]() 轴右交点
轴右交点![]() 时,
时,![]() ,
,
依题意,![]() ,解得,
,解得,![]() (舍去),或
(舍去),或![]() .
.
下面证明点![]() 对于圆
对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为一常数.
为一常数.
设![]() ,则
,则![]() ,
,
∴![]()
![]()
![]() ,
,
从而![]() 为常数.
为常数.
方法2:假设存在这样的点![]() ,使得
,使得![]() 为常数
为常数![]() ,则
,则![]() ,
,
∴![]() ,将
,将![]() 代入得,
代入得,
![]() ,即
,即
![]() 对
对![]() 恒成立,
恒成立,
∴![]() ,解得
,解得 或
或![]() (舍去),
(舍去),
所以存在点![]() 对于圆
对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为常数
为常数![]() .
.
点睛:求定值问题常见的方法有两种:
(1)从特殊入手,求出定值,再证明这个值与变量无关.
(2)直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.
【题型】解答题
【结束】
22
【题目】已知函数![]() 的导函数为
的导函数为![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,求
时,求![]() 的最大值,并推断方程
的最大值,并推断方程![]() 是否有实数解;
是否有实数解;
(2)若![]() 在区间
在区间![]() 上的最大值为-3,求
上的最大值为-3,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com