
| A.(a,b)和(b,c)内 | B.(-∞,a)和(a,b)内 |
| C.(b,c)和(c,+∞)内 | D.(-∞,a)和(c,+∞)内 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
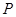 和
和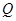 (万元),它们与投入资金
(万元),它们与投入资金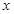 (万元)的关系依次是:其中
(万元)的关系依次是:其中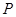 与
与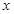 平方根成正比,且当
平方根成正比,且当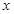 为4(万元)时
为4(万元)时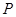 为1(万元),又
为1(万元),又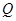 与
与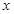 成正比,当
成正比,当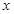 为4(万元)时
为4(万元)时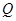 也是1(万元);某人甲有3万元资金投资.
也是1(万元);某人甲有3万元资金投资.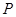 ,
,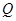 与
与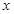 的函数关系式;
的函数关系式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
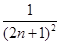 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|<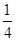 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,则当x∈(-∞,-2)时,f(x)的解析式为( )
,则当x∈(-∞,-2)时,f(x)的解析式为( )A.f(x)=- | B.f(x)=- |
C.f(x)= | D.f(x)=- |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
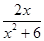 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称. 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
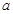 元,每期利率为
元,每期利率为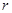 ,设本利和为
,设本利和为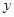 ,存期为
,存期为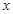 ,则
,则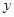 随着
随着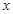 变化的函数式 .
变化的函数式 . 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com