
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .若点
.若点![]() 在椭圆
在椭圆![]() 上,则点
上,则点![]() 称为点
称为点![]() 的一个“椭点”.
的一个“椭点”.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,
, ![]() 两点的“椭点”分别为
两点的“椭点”分别为![]() ,
, ![]() ,以
,以![]() 为直径的圆经过坐标原点,试求
为直径的圆经过坐标原点,试求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1) 由![]() ,用
,用![]() 表示
表示![]() ,将点
,将点![]() 代入椭圆方程可求出
代入椭圆方程可求出![]() 的值,从而求出
的值,从而求出![]() 的值,得到椭圆的方程;(2) 设
的值,得到椭圆的方程;(2) 设![]() ,则
,则![]() ,由以
,由以![]() 为直径的圆经过坐标原点,得
为直径的圆经过坐标原点,得![]() 即
即![]() ,将直线方程代入椭圆方程,由根与系数关系得到
,将直线方程代入椭圆方程,由根与系数关系得到![]() ,代入关系式
,代入关系式![]() 得到
得到![]() 与
与![]() 的关系式
的关系式![]() ,再求出弦长
,再求出弦长![]() 与点
与点![]() 到直线
到直线![]() 的距离,即可求得三角形
的距离,即可求得三角形![]() 的面积.
的面积.
试题解析: (Ⅰ)由![]() ,得
,得![]() ,………………(1分)
,………………(1分)
又![]() ,………………(2分)
,………………(2分)
![]() 椭圆
椭圆![]() ,
,
因点![]() 在
在![]() 上,
上,  ,得
,得![]() ,…………(3分)
,…………(3分)
![]() ,………………(4分)
,………………(4分)
所以椭圆![]() 的方程为:
的方程为: ![]() ;…………(5分)
;…………(5分)
(Ⅱ)设![]() ,则
,则![]() ,
,
由以![]() 为直径的圆经过坐标原点,得
为直径的圆经过坐标原点,得![]() ,
,
即![]() (1)………………(6分)
(1)………………(6分)
由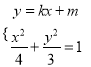 ,消除
,消除![]() 整理得:
整理得: ![]() ,
,
由![]() ,得
,得![]() ,
,
而![]() (2)………………(7分)
(2)………………(7分)
![]() (3)
(3)
将(2)(3)代入(1)得: 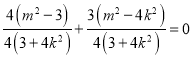 ,
,
即![]() ,………………(8分)
,………………(8分)
又 ,………………(9分)
,………………(9分)
原点![]() 到直线
到直线![]() 的距离
的距离![]() ,………………(10分)
,………………(10分)
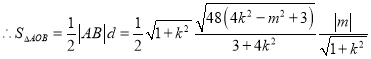 ,………………(11分)
,………………(11分)
把![]() 代入上式得
代入上式得![]() ,即
,即![]() 的面积是为
的面积是为![]() .………………(12分)
.………………(12分)


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)(i)利用(1)所求的回归方程,预测该市车流量为8万辆时![]() 的浓度;
的浓度;
(ii)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
参考公式:回归直线的方程是![]() ,其中
,其中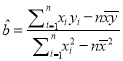 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
问题解决
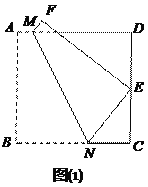
如图(1),将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C、D重合),压平后得到折痕MN.当![]() 时,求
时,求![]() 的值.
的值.
类比归纳
在图(1)中,若![]() 则
则![]() 的值等于 ;若
的值等于 ;若![]() 则
则![]() 的值等于 ;若
的值等于 ;若![]() (n为整数),则
(n为整数),则![]() 的值等于 .(用含
的值等于 .(用含![]() 的式子表示)
的式子表示)
联系拓广
如图(2),将矩形纸片ABCD折叠,使点B落在CD边上一点E(不与点C、D重合),压平后得到折痕MN设![]() ,则
,则![]() 的值等
的值等
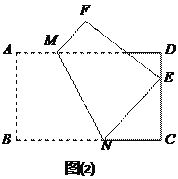
 于 ▲ .(用含
于 ▲ .(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;
(2)设![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法种数:
(1)选其中5人排成一排
(2)全体排成一排,甲不站在排头也不站在排尾
(3)全体排成一排,男生互不相邻
(4)全体排成一排,甲、乙两人中间恰好有3人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=
的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=![]() ,
,
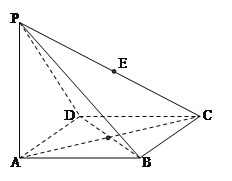
(1)求证:平面PBD⊥平面PAC;
(2)求三棱锥P--BDC的体积。
(3)在线段PC上是否存在一点E,使PC⊥平面EBD成立.如果存在,求出EC的长;如果不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com