
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a. 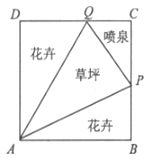
(1)当∠PAQ= ![]() 时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
(2)考虑到小区道路的整体规划,要求PB+DQ=PQ,请探究∠PAQ是否为定值,若是,求出此定值,若不是,请说明理由.
【答案】
(1)解:∵边长为1百米的正方形ABCD中,∠PAB=a,∠PAQ= ![]() ,
,
∴PB=100tanα,DQ=100tan( ![]() ﹣α﹣
﹣α﹣ ![]() )=100tan(
)=100tan( ![]() ﹣α),
﹣α),
∴S花卉种植面积=S△ABP+S△ADQ= ![]() =
= ![]() 100×100tanα+
100×100tanα+ ![]() 100tan(
100tan( ![]() ﹣α)
﹣α)
= ![]() =
= ![]() ,其中α∈[0,
,其中α∈[0, ![]() ],
],
∴当sin(2α+ ![]() )=1时,即θ=
)=1时,即θ= ![]() 时,S取得最小值为5000(2﹣
时,S取得最小值为5000(2﹣ ![]() )
)
(2)解:设∠PAB=α,∠QAD=β,CP=x,CQ=y,则BP=100﹣x,DQ=100﹣y,
在△ABP中,tanα= ![]() ,在△ADQ中,tanβ=
,在△ADQ中,tanβ= ![]() ,
,
∴tan(α+β)= ![]() =
= ![]() ,
,
∵PB+DQ=PQ,
∴100﹣x+100﹣y= ![]() ,整理可得:x+y=100+
,整理可得:x+y=100+ ![]() ,
,
∴tan(α+β)= 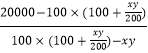 =
= 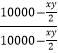 =1,
=1,
∴α+β= ![]() ,
,
∴∠PAQ是定值,且∠PAQ= ![]()
【解析】(1)由已知利用三角函数的定义可求PB=100tanα,DQ=100tan( ![]() ﹣α),利用三角形面积公式及三角函数恒等变换的应用化简可求S花卉种植面积=
﹣α),利用三角形面积公式及三角函数恒等变换的应用化简可求S花卉种植面积= ![]() ,其中α∈[0,
,其中α∈[0, ![]() ],利用正弦函数的性质可求最小值.(2)设∠PAB=α,∠QAD=β,CP=x,CQ=y,则可求BP,DQ,利用两角和的正切函数公式可求tan(α+β)=
],利用正弦函数的性质可求最小值.(2)设∠PAB=α,∠QAD=β,CP=x,CQ=y,则可求BP,DQ,利用两角和的正切函数公式可求tan(α+β)= ![]() ,由题意PB+DQ=PQ,可求:x+y=100+
,由题意PB+DQ=PQ,可求:x+y=100+ ![]() ,即可得解tan(α+β)=1,可求α+β=
,即可得解tan(α+β)=1,可求α+β= ![]() ,即可得解.
,即可得解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校开设A、B、C、D、E五门选修课,要求每位同学彼此独立地从中选修3门课程.某甲同学必选A课程,不选B课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(1)求甲同学选中C课程且乙、丙同学未选C课程的概率;
(2)用X表示甲、乙、丙选中C课程的人数之和,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣|x+a|
(1)当a=3时,解不等式f(x)≤ ![]() ;
;
(2)若关于x的不等式f(x)≤a解集为R,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某著名歌星在某地举办一次歌友会,有1000人参加,每人一张门票,每张100元.在演出过程中穿插抽奖活动,第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动.第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个实数x,y(x,y∈[0,4]),若满足y≥ ![]() ,电脑显示“中奖”,则抽奖者再次获得特等奖奖金;否则电脑显示“谢谢”,则不获得特等奖奖金.
,电脑显示“中奖”,则抽奖者再次获得特等奖奖金;否则电脑显示“谢谢”,则不获得特等奖奖金.
(1)已知小明在第一轮抽奖中被抽中,求小明在第二轮抽奖中获奖的概率;
(2)设特等奖奖金为a元,小李是此次活动的顾客,求小李参加此次活动获益的期望;若该歌友会组织者在此次活动中获益的期望值是至少获得70000元,求a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=x2﹣2ax+5.
(1)若a>1,且函数f(x)的定义域和值域均为[1,a],求实数a的值;
(2)若不等式x|f(x)﹣x2|≤1对x∈[ ![]() ,
, ![]() ]恒成立,求实数a的取值范围.
]恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为获得较好的收益,每年要投入一定资金用于广告促销,经调查,每年投入广告费![]() (百万元),可增加销售额约为
(百万元),可增加销售额约为![]() (百万元)(
(百万元)(![]() )
)
(1)若该公司当年的广告费控制在4百万元之内,则应该设入多少广告费,才能使该公司获得的收益最大?
(2)现该公司准备共投入6百万元,分别用于广告促销售和技术改造,经预测,每设入技术改造费![]() (百万元),可增加销售额约为
(百万元),可增加销售额约为![]() (百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益
(百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益![]() 销售额
销售额![]() 成本)
成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求f(x)+f(1﹣x)的值;
(2)若数列{an}满足an=f(0)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(1)(n∈N*),求数列{an}的通项公式;
)+f(1)(n∈N*),求数列{an}的通项公式;
(3)若数列{bn}满足bn=2nan , Sn是数列{bn}的前n项和,是否存在正实数k,使不等式knSn>3bn对于一切的n∈N*恒成立?若存在,请求出k的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且a2=﹣5,S5=﹣20.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求使不等式Sn>an成立的n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com