
分析 (1)由f(x)=f(x+6),可知6是函数f(x)的一个周期,则有f(3)=f(9)再由f(6)=111,组成方程组求解,可得m,n的值;
(2)运用函数周期性求得x∈[-3,3]的函数的解析式,讨论当0≤x0≤3时,当3≤x0≤6时,求得不等式的解集,即可得到所求范围;
(3)f(log3m)=f(log36)=f(6+log36),f(log3n)=f(log3110),运用已知解析式,代入再利用函数的单调性比较.
解答 解:(1)因为函数f(x)在R上满足f(x)=f(x+6),
所以6是函数f(x)的一个周期.
可得f(3)=f(9),即3-|3-m|+n=3-|9-m|+n,①
又f(6)=111,即3-|6-m|+n=111,②
联立①②组成方程组解得m=6,n=110;
(2)由(1)知,函数f(x)=3-|x-6|+110,x∈[3,9].
当-3≤x≤3,可得3≤x+6≤9,
即有f(x)=f(x+6)=3-|x|+110,x∈[-3,3],
当0≤x0≤3时,f(x0)>$\frac{331}{3}$即为3-|x0|+110>$\frac{331}{3}$,
解得-1<x0<1,即为0≤x0<1;
当3≤x0≤6时,f(x0)>$\frac{331}{3}$即为3-|x0-6|+110>$\frac{331}{3}$,
解得-1<x0-6<1,即5<x0<7,即为5<x0≤6.
综上可得,实数x0的取值范围是[0,1)∪(5,6];
(3)f(log3m)=f(log36)=f(6+log36),
由于7<6+log36<8,即有f(6+log36)=110+3-log36,
由于4<log3110<5,
则f(log3n)=f(log3110)=110+3-|log3110-6|,
=110+36-log3110,
由-log36<6-log3110,
可得f(6+log36)<f(log3110),
即为f(log3m)<f(log3n).
点评 本题主要考查函数的周期性,单调性以及用方程思想的运用,主要考查对数函数的单调性和运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
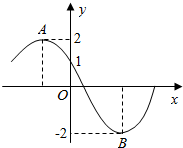 如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )| A. | 2 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆C1:x2+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右顶点分别为A,B,点P为双曲线C2:x2-$\frac{{y}^{2}}{{b}^{2}}$=1在第一象限内的图象上一点,直线AP,BP与椭圆C1分别交于C,D两点.C是AP的中点.
如图,椭圆C1:x2+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右顶点分别为A,B,点P为双曲线C2:x2-$\frac{{y}^{2}}{{b}^{2}}$=1在第一象限内的图象上一点,直线AP,BP与椭圆C1分别交于C,D两点.C是AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com