
【题目】已知函数f(x)=![]() ,g(x)=1-ax2.
,g(x)=1-ax2.
(1)若函数f(x)和g(x)的图象在x=1处的切线平行,求a的值;
(2)当x∈[0,1]时,不等式f(x)≤g(x)恒成立,求a的取值范围.
【答案】(1) a=![]() (2) a≤
(2) a≤![]()
【解析】试题分析:(1)分别求出f(x),g(x)的导数,计算得到f′(1)=g′(1),求出a的值即可;
(2)问题转化为1-a≥![]() 在[01,]恒成立,令h(x)=
在[01,]恒成立,令h(x)=![]() ,x∈[0,1],根据函数的单调性求出h(x)的最大值,得到关于a的不等式,解出即可.
,x∈[0,1],根据函数的单调性求出h(x)的最大值,得到关于a的不等式,解出即可.
试题解析:
(1)f′(x)=![]() ,f′(1)=-
,f′(1)=-![]() ,
,
g′(x)=-2ax,g′(1)=-2a,
由题意得:-2a=-![]() ,解得:a=
,解得:a=![]() ;
;
(2)当x∈[0,1]时,不等式f(x)≤g(x)恒成立,
即1-a≥![]() 在[0,1]恒成立,
在[0,1]恒成立,
令h(x)=![]() ,x∈[0,1],
,x∈[0,1],
则h′(x)=![]() ≥0,
≥0,
故h(x)在[0,1]递增,
故h(x)≤h(1)=![]() ,
,
故1-a≥![]() ,解得:a≤
,解得:a≤![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:高中数学 来源: 题型:
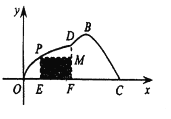
【题目】如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路![]() ,另一侧修建一条休闲大道,它的前一段
,另一侧修建一条休闲大道,它的前一段![]() 是函数
是函数![]() ,
, ![]() 的一部分,后一段
的一部分,后一段![]() 是函数
是函数![]() (
(![]() ,
, ![]() ),
),![]() 时的图象,图象的最高点为
时的图象,图象的最高点为![]() ,
, ![]() ,垂足为
,垂足为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若在草坪内修建如图所示的儿童游乐园PMFE,问点![]() 落在曲线
落在曲线![]() 上何处时,儿童乐园的面积最大?
上何处时,儿童乐园的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校5个学生的数学和物理成绩如表
学生的编号i | 1 | 2 | 3 | 4 | 5 |
数学xi | 80 | 75 | 70 | 65 | 60 |
物理yi | 70 | 66 | 68 | 64 | 62 |
(Ⅰ)假设在对这5名学生成绩进行统计时,把这5名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有2名学生的物理成绩是自己的实际分数的概率是多少?
(Ⅱ)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用x表示数学成绩,用y表示物理成绩,求y与x的回归方程;
参考公式: ![]() =
= 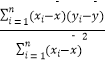 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,其中0<ω<2; (Ⅰ)若f(x)的最小正周期为π,求f(x)的单调增区间;
,其中0<ω<2; (Ⅰ)若f(x)的最小正周期为π,求f(x)的单调增区间;
(Ⅱ)若函数f(x)的图象的一条对称轴为 ![]() ,求ω的值.
,求ω的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|+2x.
(1)若函数f(x)在R上是增函数,求实数a的取值范围;
(2)求所有的实数a,使得对任意x∈[1,2]时,函数f(x)的图象恒在函数g(x)=2x+1图象的下方;
(3)若存在a∈[﹣4,4],使得关于x的方程f(x)=tf(a)有三个不相等的实数根,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣2ax2+3a2x+b(a>0).
x3﹣2ax2+3a2x+b(a>0).
(1)当y=f(x)的极小值为1时,求b的值;
(2)若f(x)在区间[1,2]上是减函数,求a的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx﹣ ![]() )+1(A>0,ω>0)的最大值为3,其图象的相邻两条对称轴之间的距离为
)+1(A>0,ω>0)的最大值为3,其图象的相邻两条对称轴之间的距离为 ![]() .
.
(1)求函数f(x)对称中心的坐标;
(2)求函数f(x)在区间[0, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】偶函数y=f(x)在区间[﹣4,0]上单调递增,则有( )
A.f(﹣1)>f( ![]() )>f(﹣π)
)>f(﹣π)
B.f( ![]() )>f(﹣1)>f(﹣π)
)>f(﹣1)>f(﹣π)
C.f(﹣π)>f(﹣1)>f( ![]() )
)
D.f(﹣1)>f(﹣π)>f( ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com