
【题目】在数列![]() 中,
中,![]() ,且
,且![]() .
.
(1)![]() 的通项公式为__________;
的通项公式为__________;
(2)在![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这
这![]() 项中,被
项中,被![]() 除余
除余![]() 的项数为__________.
的项数为__________.
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() . 对于函数
. 对于函数![]() 、
、![]() ,若存在常数
,若存在常数![]() ,
,![]() ,使得
,使得![]() ,不等式
,不等式![]() 都成立,则称直线是
都成立,则称直线是![]() 函数
函数![]() 与
与![]() 的分界线.
的分界线.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,试探究函数
时,试探究函数![]() 与
与![]() 是否存在“分界线”?若存在,求出分界线方程;若不存在说明理由.
是否存在“分界线”?若存在,求出分界线方程;若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数![]() 是反映空气质量状况的指数,
是反映空气质量状况的指数,![]() 指数值越小,表明空气质量越好,其对应关系如表:
指数值越小,表明空气质量越好,其对应关系如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市10月1日—20日![]() 指数变化趋势:
指数变化趋势:
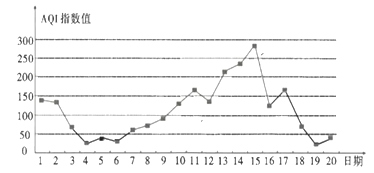
下列叙述正确的是( )
A.该市10月的前半个月的空气质量越来越好
B.这20天中的中度污染及以上的天数占![]()
C.这20天中![]() 指数值的中位数略高于100
指数值的中位数略高于100
D.总体来说,该市10月上旬的空气质量比中旬的空气质量差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ax﹣ex(a∈R),g(x)=![]() .
.
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)x0∈(0,+∞),使不等式f (x)≤g(x)﹣ex成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 m、n 是两条不同的直线,α、β、γ是三个不同的平面,下列命题中正确的是( )
A.若α⊥β , β⊥γ ,则α∥γ
B.若 ![]() ,
, ![]() , m∥n ,则α∥β
, m∥n ,则α∥β
C.若 m、n 是异面直线, ![]() , m∥β ,
, m∥β , ![]() , n∥α ,则α∥β
, n∥α ,则α∥β
D.平面α内有不共线的三点到平面 β的距离相等,则α∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
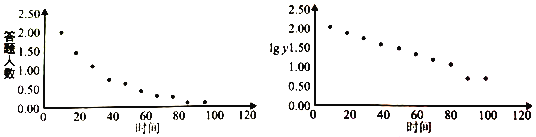
【题目】一个调查学生记忆力的研究团队从某中学随机挑选100名学生进行记忆测试,通过讲解100个陌生单词后,相隔十分钟进行听写测试,间隔时间![]() (分钟)和答对人数
(分钟)和答对人数![]() 的统计表格如下:
的统计表格如下:
时间 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
答对人数 | 98 | 70 | 52 | 36 | 30 | 20 | 15 | 11 | 5 | 5 |
| 1.99 | 1.85 | 1.72 | 1.56 | 1.48 | 1.30 | 1.18 | 1.04 | 0.7 | 0.7 |
时间![]() 与答对人数
与答对人数![]() 的散点图如图:
的散点图如图:
附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对于一组数据
,对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: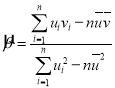 ,
,![]() .请根据表格数据回答下列问题:
.请根据表格数据回答下列问题:
(1)根据散点图判断,![]() 与
与![]() ,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果,建立![]() 与
与![]() 的回归方程;(数据保留3位有效数字)
的回归方程;(数据保留3位有效数字)
(3)根据(2)请估算要想记住![]() 的内容,至多间隔多少分钟重新记忆一遍.(参考数据:
的内容,至多间隔多少分钟重新记忆一遍.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域均为D的三个函数f(x),g(x),h(x)满足条件:对任意x∈D,点(x,g(x)与点(x,h(x)都关于点(x,f(x)对称,则称h(x)是g(x)关于f(x)的“对称函数”.已知g(x)=![]() ,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是_____.
,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是函数
是函数![]() 定义域的一个子集,若存在
定义域的一个子集,若存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 的一个“准不动点”,也称
的一个“准不动点”,也称![]() 在区间
在区间![]() 上存在准不动点,已知
上存在准不动点,已知![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的准不动点;
的准不动点;
(2)若函数![]() 在区间
在区间![]() 上存在准不动点,求实数
上存在准不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com