
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的极值;
的极值;
(Ⅱ)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(Ⅲ)若对于任意的![]() 都有
都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时, ![]() 取得极小值为
取得极小值为![]() ,无极大值.;(Ⅱ)当
,无极大值.;(Ⅱ)当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上是减函数,在
上是减函数,在![]() 上是增函数,当
上是增函数,当![]() 时,
时, ![]() 在
在![]() 上是减函数,当
上是减函数,当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上是减函数,在
上是减函数,在![]() 上是增函数;(Ⅲ)
上是增函数;(Ⅲ) ![]() .
.
【解析】试题分析:
(Ⅰ) 当![]() 时,
时, ![]() ,定义域为
,定义域为![]() ,
, ![]() .据此可得当
.据此可得当![]() 时,
时, ![]() 取得极小值为
取得极小值为![]() ,无极大值.
,无极大值.
(Ⅱ) 当![]() 时,函数的定义域为
时,函数的定义域为![]() ,且
,且![]() .分类讨论有:
.分类讨论有:
(1)当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
(2)当![]() 时,
时, ![]() 在
在![]() 上是减函数;
上是减函数;
(3)当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上是减函数,在
上是减函数,在![]() 上是增函数
上是增函数
(Ⅲ) 由(Ⅱ)知,当![]() 时,
时, ![]() 在
在![]() 上是减函数.原问题等价于
上是减函数.原问题等价于![]() 对任意
对任意![]() 恒成立,分离参数有
恒成立,分离参数有![]() 对任意
对任意![]() 恒成立.据此可得实数
恒成立.据此可得实数![]() 的取值范围为
的取值范围为![]() .
.
试题解析:
(Ⅰ)当![]() 时,
时, ![]() ,定义域为
,定义域为![]() ,
,
![]() 的导函数
的导函数![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是增函数.
上是增函数.
∴当![]() 时,
时, ![]() 取得极小值为
取得极小值为![]() ,无极大值.
,无极大值.
(Ⅱ)当![]() 时,
时, ![]() 的定义域为
的定义域为![]() ,
, ![]() 的导函数为
的导函数为![]() .
.
由![]() 得
得![]() ,
, ![]() ,
, ![]() .
.
(1)当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
(2)当![]() 时,
时, ![]() 在
在![]() 上是减函数;
上是减函数;
(3)当![]() 时,
时, ![]() 在
在![]() 和
和![]() 上是减函数,在
上是减函数,在![]() 上是增函数
上是增函数
(Ⅲ)由(Ⅱ)知,当![]() 时,
时, ![]() 在
在![]() 上是减函数.
上是减函数.
∴![]() .
.
∵对于任意的![]() 都有
都有![]() ,
,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() 对任意
对任意![]() 恒成立.
恒成立.
当![]() 时,
时, ![]() ,∴
,∴![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,﹣2),N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)问是否存在满足以下两个条件的直线l:①斜率为1;②直线被圆C截得的弦为AB,以AB为直径的圆C1过原点.若存在这样的直线,请求出其方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 和直线
和直线![]() :
: ![]() ,椭圆的离心率
,椭圆的离心率![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() .
.

(Ⅰ)求椭圆的方程;
(Ⅱ)已知定点![]() ,若直线
,若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点,试判断是否存在直线
两点,试判断是否存在直线![]() ,使以
,使以![]() 为直径的圆过点
为直径的圆过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C= ![]() . (Ⅰ)若△ABC的面积等于
. (Ⅰ)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(Ⅱ)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱。现统计了连续5天的售出和收益情况,如下表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(Ⅰ) 若x与y成线性相关,则某天售出8箱水时,预计收益为多少元?
(Ⅱ) 期中考试以后,学校决定将诚信用水的收益,以奖学金的形式奖励给品学兼优的特困生,规定:特困生考入年级前200名,获一等奖学金500元;考入年级201—500 名,获二等奖学金300元;考入年级501名以后的特困生将不获得奖学金。甲、乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() .
.
⑴在学生甲获得奖学金条件下,求他获得一等奖学金的概率;
⑵已知甲、乙两名学生获得哪个等第的奖学金是相互独立的,求甲、乙两名学生所获得奖学金总金额X 的分布列及数学期望。
附: 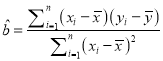 ,
, ![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC. 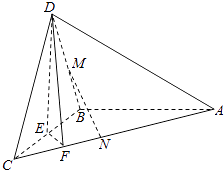
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN= ![]() CA,求证:MN∥平面DEF.
CA,求证:MN∥平面DEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com