【题目】设
为实数，函数
.
（1）求证： 
不是
上的奇函数；
（2）若
是
上的单调函数，求实数
的值；
（3）若函数
在区间
上恰有3个不同的零点，求实数
的取值范围.
【答案】（1）证明见解析；（2）
；（3）
.
【解析】试题分析：（1）由
无解，即可得结论；（2）分三种情况讨论，结合二次函数的图像及单调性，排除不合题意的
值即可.（3）三种情况分别结合函数单调性判断出函数零点个数，即可得出结果.
试题解析：（1）假设
是
上的奇函数，
则对任意的
，都有
（*）
取
，得
，即
，解得
，
此时
，所以
，从而
，
这与（*）矛盾，所以假设不成立，所以
不是
上的奇函数；
（2）
，
①当
时，对称轴
，所以
在
上单调递减，在
上单调递增，在
上单调递减，不符；
②当
时，对称轴
，所以
在
上单调递减，在
上单调递增，在
上单调递减，不符；
③当
时，对称轴
，所以
在
上单调递减，在
上单调递减，所以
是
上的单调减函数．
综上， 
．
（3）①当
时，由（2）知， 
是
上的单调减函数，至多1个零点，不符；
②当
时，由（2）知， 
，所以
在
上单调递减，
所以
在
上至多1个零点，不符；
③当
时，由（2）知， 
，所以
在
上单调递减，在
上单调递增，在
上单调递减．
因为
在区间
上恰有3个零点，
所以
，
，解得
或
，又
，故
，综上，实数
的取值范围是
．
科目：高中数学 来源： 题型：
【题目】已知三棱柱ABC-A1B1C1中，侧棱垂直于底面,AC=BC,点D是AB的中点．
(1)求证：BC1∥平面CA1D；(2)若底面ABC为边长为2的正三角形，BB1=
求三棱锥B1-A1DC的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高校大一新生中的6名同学打算参加学校组织的“雅荷文学社”、“青春风街舞社”、“羽乒协会”、“演讲团”、“吉他协会”五个社团，若每名同学必须参加且只能参加1个社团且每个社团至多两人参加，则这6个人中至多有1人参加“演讲团”的不同参加方法数为（ ）
A. 4680 B. 4770 C. 5040 D. 5200
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）当
时，求函数
的单调区间；
（2）当
时，若
对任意
恒成立，求实数
的取值范围；
（3）设函数
的图象在两点
处的切线分别为
，若
，且
，求实数
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂2万元设计了某款式的服装，根据经验，每生产1百套该款式服装的成本为1万元，每生产
（百套）的销售额（单位：万元）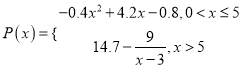
.
（1）若生产6百套此款服装，求该厂获得的利润；
（2）该厂至少生产多少套此款式服装才可以不亏本？
（3）试确定该厂生产多少套此款式服装可使利润最大，并求最大利润.（注：利润=销售额-成本，其中成本=设计费+生产成本）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】亳州某商场举行购物抽奖活动，规定每位顾客从装有编号为0，1，2，3四个相同小求的抽奖箱中，每次取出一球，记下编号后放回，连续取两次，若取出的两个小球号码相加之和等于6，则中一等奖；等于5中二等奖；等于4或3中三等奖.
（1）求中三等奖的概率；
（2）求不中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
