Question

某旅馆有相同标准的床铺100张，根据经验，当旅馆的床价（即每床每天的租金）不超过10元时，床位可以全部租出，当床价高于10元，每提高1元，将有3张床空置．旅馆定价条件是：（1）床价为1元的整数倍；（2）该旅馆每天支出为575元，床位出租收入必须高于支出．若用x表示床价，y表示每天出租床位的净收入（即除去每天支出后的收入）．
①把y表示成x的函数，并求出其定义域；
②如何定价，该旅馆每天净收入最多？

Answer 1

解：①依题意x∈N*，100x＞575，
所以x≥6，当6≤x≤10时，y=100x-575；x＞10时，
由x[100-3（x-10）]＞575和x∈N*，
解得x≤38，当10＜x≤38时，y=x[100-3（x-10）]-575=-3x²+130x-575．
综上所述，．
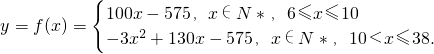
②二次函数y=-3x²+130x-575的对称轴，
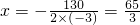
因为x∈N*，直接计算知f（10）=425，f（21）=832，f（22）=833，
比较得：每床每天的租金为22元时，该旅馆每天净收入最多．
分析：①分价格不高与10元和高于10元两种情况分析，当不高于10元时，有100x＞575，即当6≤x≤10时，y=100x-575；当高于10元时有x[100-3（x-10）]＞575和x∈N*，即当10＜x≤38时，y=x[100-3（x-10）]-575=-3x²+130x-575．
②由①知函数是分段函数，所以每一段取得取大值，从中取最大的作为函数的最大值，同时也就明确了最大时的定价．
点评：本题主要考查分段函数模型的建立和应用，还考查了分段函数求最值，方法是每一段求得最大值，再从中取最大的作为函数的最大值，同时，确定函数关系实质就是将文字语言转化为数学符号语言--数学化，再用数学方法定量计算得出所要求的结果，关键是理解题意，将变量的实际意义符号化．
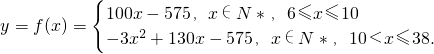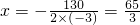