
【题目】探究函数![]() 的图像时,列表如下:
的图像时,列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
观察表中y值随x值的变化情况,完成以下的问题:
(1)函数![]() 的递减区间是 ,递增区间是 ;
的递减区间是 ,递增区间是 ;
(2)若对任意的![]() 恒成立,试求实数m的取值范围.
恒成立,试求实数m的取值范围.
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
(1) 已知![]() ,
,![]() ,
,![]() ,则
,则![]()
(2)将6个相同的小球放入4个不同的盒子中,要求不出现空盒,共有10种放法.
(3) ![]() 被
被![]() 除后的余数为
除后的余数为![]() .
.
(4) 若![]() ,则
,则![]() =
=![]()
(5)抛掷两个骰子,取其中一个的点数为点![]() 的横坐标,另一个的点数为点
的横坐标,另一个的点数为点![]() 的纵坐标,连续抛掷这两个骰子三次,点
的纵坐标,连续抛掷这两个骰子三次,点![]() 在圆
在圆![]() 内的次数
内的次数![]() 的均值为
的均值为![]()
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由实数构成的等比数列{an}满足a1=2,a1+ a3+ a5=42.
(I)求数列{an}的通项公式;
(II)求a2+ a4+ a6+…+ a2n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)令![]() ,试讨论
,试讨论![]() 的单调性;
的单调性;
(2)若对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由![]() ,对函数求导,研究导函数的正负得到单调性即可;(2)由条件可知
,对函数求导,研究导函数的正负得到单调性即可;(2)由条件可知![]() 对
对![]() 恒成立,变量分离
恒成立,变量分离![]() ,令
,令![]() ,求这个函数的最值即可.
,求这个函数的最值即可.
解析:
(1)由![]() 得
得![]()
当![]() 时,
时, ![]() 恒成立,则
恒成立,则![]() 单调递减;
单调递减;
当![]() 时,
时,  ,令
,令 ,
,
令 .
.
综上:当![]() 时,
时, ![]() 单调递减,无增区间;
单调递减,无增区间;
当![]() 时,
时,  ,
, 
(2)由条件可知![]() 对
对![]() 恒成立,则
恒成立,则
当![]() 时,
时, ![]() 对
对![]() 恒成立
恒成立
当![]() 时,由
时,由![]() 得
得![]() .令
.令![]() 则
则
 ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]()
所以![]() ,从而可知
,从而可知![]() .
.
综上所述: 所求![]() .
.
点睛:导数问题经常会遇见恒成立的问题:
(1)根据参变分离,转化为不含参数的函数的最值问题;
(2)若 ![]() 就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为
就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为![]() ,若
,若![]() 恒成立
恒成立![]() ;
;
(3)若![]() 恒成立,可转化为
恒成立,可转化为![]() (需在同一处取得最值) .
(需在同一处取得最值) .
【题型】解答题
【结束】
22
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴的极坐标系中,直线
轴的非负半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·绍兴仿真考试)已知数列{an}的奇数项依次构成公差为d1的等差数列,偶数项依次构成公差为d2的等差数列(其中d1,d2为整数),且对任意n∈N*,都有an<an+1,若a1=1,a2=2,且数列{an}的前10项和S10=75,则d1=________,a8=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
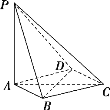
【题目】如图,在四棱锥PABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
(1)求证:BD⊥平面PAC;
(2)若PA=4,求平面PBC与平面PDC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个以A1B1C1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:

(1)该几何体的体积.
(2)截面ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com