Question

【题目】已知方程有且只有两个解，，则以下判断正确的是

A. B.

C. D.

Answer 1

【答案】D

【解析】

由题意知函数f（x）＝lnx﹣2ax+1的图象与x轴有两个交点，设f（x）＝lnx﹣2ax+1，由导数的运算得：a＞0且f（x）在区间（0，）为增函数，在区间（，+∞）为减函数，由图象知f（x）max＝f（）＝﹣ln2a＞0，结合f（1）＝1﹣2a＞0，得到选项.

设f（x）＝lnx﹣2ax+1，

则f′（x）2a，

①当a≤0时，f′（x）＞0，f（x）在（0，+∞）为增函数，显然不满足题意．

②当a＞0时，

由0时，f′（x）＞0，由x时，f′（x）＜0，

得f（x）在区间（0，）为增函数，在区间（，+∞）为减函数，

即f（x）max＝f（）＝﹣ln2a，

由方程lnx+1＝2ax有且只有两个解x1，x2（x1＜x2），

即f（x）＝lnx﹣2ax+1的图象与x轴有两个交点，

即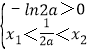，即x1x2且0＜2a＜1，③

又f（1）＝1﹣2a＞0，

由零点定理可得，x1＜1④

结合③④得：，

故选：D．