
【题目】
设![]() 为实数,函数
为实数,函数![]() 。
。
(1)求![]() 的单调区间与极值;
的单调区间与极值;
(2)求证:当![]() 且
且![]() 时,
时,![]() 。
。
【答案】(1)见解析;(2)见解析.
【解析】
试题(1)由![]() ,知
,知![]() .令
.令![]() ,得
,得![]() .列表讨论能求出
.列表讨论能求出![]() 的单调区间区间及极值.
的单调区间区间及极值.
(2)设![]() ,于是
,于是![]() ,由(1)知当
,由(1)知当![]() 时,
时,![]() 最小值为
最小值为![]() ,于是对任意
,于是对任意![]() ,都有
,都有![]() ,所以
,所以![]() 在
在![]() 内单调递增.由此能够证明
内单调递增.由此能够证明![]() .
.
试题解析:解:∵f(x)=ex﹣2x+2a,x∈R,
∴f′(x)=ex﹣2,x∈R.
令f′(x)=0,得x=ln2.
于是当x变化时,f′(x),f(x)的变化情况如下表:

故f(x)的单调递减区间是(﹣∞,ln2),
单调递增区间是(ln2,+∞),
f(x)在x=ln2处取得极小值,
极小值为f(ln2)=eln2﹣2ln2+2a=2(1﹣ln2+a),无极大值.
(2)证明:设g(x)=ex﹣x2+2ax﹣1,x∈R,
于是g′(x)=ex﹣2x+2a,x∈R.
由(1)知当a>ln2﹣1时,
g′(x)最小值为g′(ln2)=2(1﹣ln2+a)>0.
于是对任意x∈R,都有g′(x)>0,所以g(x)在R内单调递增.
于是当a>ln2﹣1时,对任意x∈(0,+∞),都有g(x)>g(0).
而g(0)=0,从而对任意x∈(0,+∞),g(x)>0.
即ex﹣x2+2ax﹣1>0,
故ex>x2﹣2ax+1.


科目:高中数学 来源: 题型:
【题目】如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”.现提供4种颜色给“弦图”的5个区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有( )
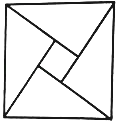
A.48种B.72种C.96种D.144种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,已知
两点,已知![]()
![]() ,
,![]()
![]() ,若椭圆的离心率
,若椭圆的离心率![]() ,又经过点
,又经过点![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆的方程;
(2)当![]() 时,试问:
时,试问:![]() 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国际海洋安全规定:两国军舰正常状况下(联合军演除外),在公海上的安全距离为20![]() (即距离不得小于20
(即距离不得小于20![]() ),否则违反了国际海洋安全规定.如图,在某公海区域有两条相交成60°的直航线
),否则违反了国际海洋安全规定.如图,在某公海区域有两条相交成60°的直航线![]() ,
,![]() ,交点是
,交点是![]() ,现有两国的军舰甲,乙分别在
,现有两国的军舰甲,乙分别在![]() ,
,![]() 上的
上的![]() ,
,![]() 处,起初
处,起初![]() ,
,![]() ,后来军舰甲沿
,后来军舰甲沿![]() 的方向,乙军舰沿
的方向,乙军舰沿![]() 的方向,同时以40
的方向,同时以40![]() 的速度航行.
的速度航行.
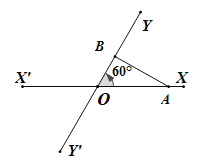
(1)起初两军舰的距离为多少?
(2)试判断这两艘军舰是否会违反国际海洋安全规定?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Fibonacci数列又称黄金分割数列,因为当n趋向于无穷大时,其相邻两项中的前项与后项的比值越来越接近黄金分割数![]() .已知Fibonacci数列的递推关系式为
.已知Fibonacci数列的递推关系式为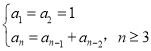 .
.
(1)证明:Fibonacci数列中任意相邻三项不可能成等比数列;
(2)Fibonacci数列{an}的偶数项依次构成一个新数列,记为{bn},证明:{bn+1-H2·bn}为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 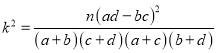 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com