
![]() 直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.
直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)过A、B两点分别作此抛物线的切线,两切线相交于N点.
求证:![]() ;
;
(Ⅲ)若p是不为1的正整数,当![]() ,△ABN的面积的取值范围为[5
,△ABN的面积的取值范围为[5![]() ,20
,20![]() ]时,求该抛物线的方程.
]时,求该抛物线的方程.
(Ⅰ)![]() ·
·![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)证明见解析
(Ⅲ)抛物线的方程:x2=4y.
(Ⅰ)由条件得M(0,-![]() ),F(0,
),F(0,![]() ).设直线AB的方程为
).设直线AB的方程为
y=kx+![]() ,A(
,A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() )
)
则![]() ,
,![]() ,Q(
,Q(![]() ). …………………………2分
). …………………………2分
由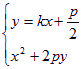 得
得![]() .
.
∴由韦达定理得![]() +
+![]() =2pk,
=2pk,![]() ·
·![]() =-
=-![]() …………………………3分
…………………………3分
从而有![]()
![]() =
=![]()
![]() +
+![]() =k(
=k(![]() +
+![]() )+p=2pk
)+p=2pk![]() ÷p.
÷p.
∴![]() ·
·![]() 的取值范围是
的取值范围是![]() . …………………………4分
. …………………………4分
(Ⅱ)抛物线方程可化为![]() ,求导得
,求导得![]() .
.
∴![]()
![]()
![]() =y
=y ![]() .
.
∴切线NA的方程为:y-![]() 即
即![]() .
.
切线NB的方程为:![]() …………………………6分
…………………………6分
由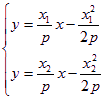 解得
解得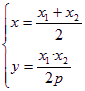 ∴N(
∴N(![]() )
)
从而可知N点Q点的横坐标相同但纵坐标不同.
∴NQ∥OF.即![]() …………………………7分
…………………………7分
又由(Ⅰ)知![]() +
+![]() =2pk,
=2pk,![]() ·
·![]() =-p
=-p![]()
∴N(pk,-![]() ). …………………………8分
). …………………………8分
而M(0,-![]() ) ∴
) ∴![]()
又![]() . ∴
. ∴![]() . …………………………9分
. …………………………9分
(Ⅲ)由![]() .又根据(Ⅰ)知
.又根据(Ⅰ)知![]()
∴4p![]() =p
=p![]() k
k![]() ,而p>0,∴k
,而p>0,∴k![]() =4,k=±2. …………………………10分
=4,k=±2. …………………………10分
由于![]() =(-pk,p),
=(-pk,p), ![]()
∴![]()
从而![]() . …………………………11分
. …………………………11分
又|![]() |=
|=![]() ,|
,|![]() |=
|=![]()
∴![]() .
.
而![]() 的取值范围是[5
的取值范围是[5![]() ,20
,20![]() ].
].
∴5![]() ≤5
≤5![]() p2≤20
p2≤20![]() ,1≤p2≤4. …………………………13分
,1≤p2≤4. …………………………13分
而p>0,∴1≤p≤2.
又p是不为1的正整数.
∴p=2.
故抛物线的方程:x2=4y. …………………………14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| MA |
| MB |
| MN |
| OF |
| NQ |
| OF |
| MA |
| MB |
| 5 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
![]() 直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.
直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)过A、B两点分别作此抛物线的切线,两切线相交于N点.
求证:![]() ;
;
(Ⅲ)若p是不为1的正整数,当![]() ,△ABN的面积的取值范围为[5
,△ABN的面积的取值范围为[5![]() ,20
,20![]() ]时,求该抛物线的方程.
]时,求该抛物线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证![]() 的取值范围;
的取值范围;
(2)过A、B两点分别作此抛物线的切线,两切线相交于N点,
求证:![]() ;
;
(3)设直线AB与x轴、y轴的两个交点分别为K和L,当![]() =4p2,△ABN的面积的取值范围限定为[
=4p2,△ABN的面积的取值范围限定为[![]() ]时,求动线段KL的轨迹所形成的平面区域的面积.
]时,求动线段KL的轨迹所形成的平面区域的面积.
查看答案和解析>>
科目:高中数学 来源:2011年广东省高考数学第三轮复习精编模拟试卷08(理科)(解析版) 题型:解答题
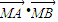 的取值范围;
的取值范围;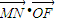 =0,
=0,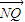 ∥
∥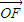 ;
;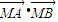 =4P2,△ABN的面积的取值范围为[5
=4P2,△ABN的面积的取值范围为[5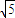 ,20
,20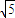 ]时,求该抛物线的方程.
]时,求该抛物线的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com