
分析 由已知推导出{$\frac{{S}_{n}}{n}$}是以-2015为首项,以1为公差的等差数列.由此能求出S2015.
解答 解:设等差数列前n项和为Sn=An2+Bn,
则 $\frac{{S}_{n}}{n}$=An+B,∴{$\frac{{S}_{n}}{n}$}成等差数列.
∵$\frac{{S}_{1}}{1}=\frac{{a}_{1}}{1}$=-2015,∴{$\frac{{S}_{n}}{n}$}是以-2015为首项,以1为公差的等差数列.
∴$\frac{{S}_{2015}}{2015}=-2015+2014×1$=-1,
∴S2015=-2015.
故答案为:-2015.
点评 本题考查数列的前2015项和的求法,是基础题,解题时要认真审题,注意构造法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | [-10,2] | B. | [-14,-2] | C. | (-∞,-2] | D. | [-14,-5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 101 101 | B. | 11 011 011 | C. | 1 101 111 | D. | 1 011 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
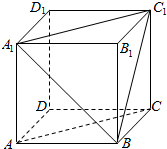 如图,在正方体A1B1C1D1-ABCD中,
如图,在正方体A1B1C1D1-ABCD中,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com