
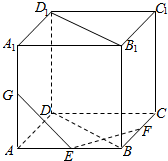
 如图,在棱长为2的正方体ABCD一A1B1C1D1中,点E,F,G分别是边AB,BC,AA1上的点,记AE=x,BF=y,A1G=z,
如图,在棱长为2的正方体ABCD一A1B1C1D1中,点E,F,G分别是边AB,BC,AA1上的点,记AE=x,BF=y,A1G=z,分析 (1)若x=y=z=1,平面EFG与边CC1的交点H为CC1的中点,取CD的中点O,则A1E∥D1O,即可求异面直线A1E与DH所成的角;
(2)若x+y=2,则BE=BF,证明EF⊥平面BDD1B1,即可证明截面EFG⊥平面BDD1B1;
(3)三棱锥B1-GEF的体积=三棱锥F-GEB1的体积=$\frac{1}{3}$${S}_{△GE{B}_{1}}$•BF,求出${S}_{△GE{B}_{1}}$的最小值,即可求三棱锥B1-GEF的体积的最小值.
解答 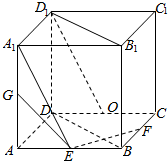 (1)解:由题意,平面EFG与边CC1的交点H为CC1的中点,取CD的中点O,则A1E∥D1O,
(1)解:由题意,平面EFG与边CC1的交点H为CC1的中点,取CD的中点O,则A1E∥D1O,
正方形CDD1C1中,△D1DO≌△DCH,∴∠OD1D=∠HDC,∴DH⊥D1O
∴DH⊥A1E,
∴异面直线A1E与DH所成的角为90°;
(2)证明:x+y=2,则BE=BF,∴EF⊥BD,
∵EF⊥D1D,D1D∩BD=D,
∴EF⊥平面BDD1B1,
∵EF?截面EFG,
∴截面EFG⊥平面BDD1B1;
(3)解:三棱锥B1-GEF的体积=三棱锥F-GEB1的体积=$\frac{1}{3}$${S}_{△GE{B}_{1}}$•BF.
${S}_{△GE{B}_{1}}$=4-$\frac{1}{2}•2•x$-$\frac{1}{2}•x•(2-x)$-$\frac{1}{2}•2•(2-x)$=$\frac{1}{2}(x-1)^{2}+\frac{3}{2}$,
∴x=1时,${S}_{△GE{B}_{1}}$的最小值为$\frac{3}{2}$,
∴三棱锥B1-GEF的体积的最小值为$\frac{1}{2}$.
点评 本题考查异面直线A1E与DH所成的角,考查平面与平面垂直,考查三棱锥B1-GEF的体积,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{x-1}$•$\sqrt{x+3}$,g(x)=$\sqrt{{x}^{2}+2x-3}$ | B. | f(x)=$\frac{{x}^{2}-2x+1}{x-1}$,g(x)=x-1 | ||
| C. | f(x)=$\frac{\sqrt{1-{x}^{2}}}{|x+2|}$,g(x)=$\frac{\sqrt{1-{x}^{2}}}{x+2}$ | D. | 以上三组都不是同一函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,BC=8,AB=10,O为BC上一点,以O为圆心,OB为半径作半圆与BC边、AB边分别交于点D、E,连结DE.
如图,在△ABC中,∠C=90°,BC=8,AB=10,O为BC上一点,以O为圆心,OB为半径作半圆与BC边、AB边分别交于点D、E,连结DE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
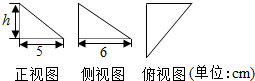
| A. | 25xcm2 | B. | $\frac{77π}{2}$cm2 | C. | 77πcm2 | D. | 144πcm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com