
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且B是A,C的等差中项.
(1)若![]() ,求边c的值;
,求边c的值;
(2)设t=sinAsinC,求t的取值范围.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)由已知利用等差中项的性质,三角形内角和定理可求B的值,进而根据余弦定理可得c2﹣3c﹣4=0,解方程可得c的值.
(2)由已知利用三角函数恒等变换的应用,可求t=![]() sin(2A﹣
sin(2A﹣![]() ,根据正弦函数的性质可求其取值范围.
,根据正弦函数的性质可求其取值范围.
(1)∵B是A,C的等差中项,
∴2B=A+C,
∵A+B+C=π,
∴B=![]() ,
,
∵b=![]() ,a=3,又b2=a2+c2﹣2accosB,
,a=3,又b2=a2+c2﹣2accosB,
∴c2﹣3c﹣4=0,
解得c=4,或c=﹣1(舍去),故c=4.
(2)∵A+C=![]() ,
,
∴t=sinAsin(![]() ﹣A)=sinA(
﹣A)=sinA(![]() cosA+
cosA+![]() sinA)=
sinA)=![]() sin(2A﹣
sin(2A﹣![]() ,
,
∵A∈(0,![]() ),2A﹣
),2A﹣![]() ∈(﹣
∈(﹣![]() ),
),
sin(2A﹣![]() )∈(
)∈(![]() ,1],
,1],
故t的取值范围为(0,![]() ].
].


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】某娱乐节目参赛选手分初赛培训、复赛三个阶段选拔,将50位参选手的初赛成绩(总分150分)分成[90,100),[100,110),[110,120),[120,130),[130,140)5组进行统计,得到如图所示的频率分布直方图.
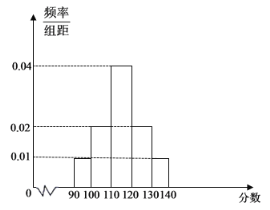
(1)根据频率分析直方图,估算这50个选手初赛成绩的平均分,若节日组规定成绩大于或等于120分的选手可获得节目组组织的培训资格,120分以下(不包括120)的则被淘汰,求这50个人中获得培训资格的人数;
(2)节目组从获得培训资格的人员中选拔部分人员进入复赛.为增加节目的娱乐性,节目组提供了以下两种进入复赛的方式(每位选手只能选择其中一种)
第一种方式:利用分层抽样的方法抽取6名选手参加复赛;
第二种方式:每人最多有5次答题机会,累计答对3题或答错3题终止答题,答对3题可参加复赛
①已知甲的初赛成绩在[120,130)内,他答对每一个问题的概率为![]() ,并且互相之间没有影响甲要想参加复赛,选择那种方式更有利?
,并且互相之间没有影响甲要想参加复赛,选择那种方式更有利?
②若甲选择第二种方式,求他在答题过程中答题个数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月24日国家统计局在庆祝中华人民共和国成立70周年活动新闻中心举办新闻发布会指出,1952年~2018年,我国GDP查679.1亿元跃升至90.03万亿元,实际增长174倍;人均GDP从119元提高到6.46万元,实际增长70倍.全国各族人民,砥砺奋进,顽强拼搏,实现了经济社会的跨越式发展.如图是全国2010年至2018年GDP总量![]() (万亿元)的折线图.注:年份代码1~9分别对应年份2010~2018.
(万亿元)的折线图.注:年份代码1~9分别对应年份2010~2018.
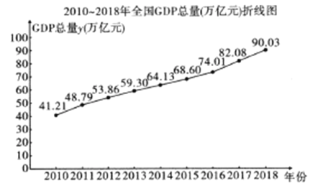
(1)由折线图看出,可用线性回归模型拟合![]() 与年份代码
与年份代码![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),并预测2021年全国GDP的总量.
的回归方程(系数精确到0.01),并预测2021年全国GDP的总量.
附注:参考数据:![]() .
.
参考公式:相关系数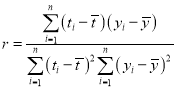 ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为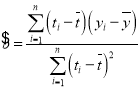 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:其中所有假命题的序号是_______.
①命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ;
;
②将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像;
的图像;
③幂函数![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() ;
;
④函数![]() 有两个零点.
有两个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 和到直线
和到直线![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点作垂直于
,过点作垂直于![]() 轴的直线与曲线
轴的直线与曲线![]() 相交于两点,直线
相交于两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 相交于一点(交点位于线段
相交于一点(交点位于线段![]() 上,且与
上,且与![]() 不重合).
不重合).
(1)求曲线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切时,四边形
相切时,四边形![]() 的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 与点
与点![]() 均在椭圆
均在椭圆![]() 上,且
上,且![]() 关于原点对称,问:椭圆上是否存在点
关于原点对称,问:椭圆上是否存在点![]() (点
(点![]() 在一象限),使得
在一象限),使得![]() 为等边三角形?若存在,求出点
为等边三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型歌手选秀活动,过程分为初赛、复赛和决赛.经初赛进入复赛的40名选手被平均分成甲、乙两个班,由组委会聘请两位导师各负责一个班进行声乐培训.下图是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图.赛制规定:参加复赛的40名选手中,获得的支持票数不低于85票的可进入决赛,其中票数不低于95票的选手在决赛时拥有“优先挑战权”.
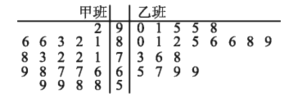
(1)从进入决赛的选手中随机抽出2名,X表示其中拥有“优先挑战权”的人数,求X的分布列和数学期望;
(2)请填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关?
列联表,并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关?
甲班 | 乙班 | 合计 | |
进入决赛 | |||
未进入决赛 | |||
合计 |
下面的临界值表仅供参考:
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: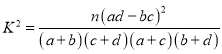 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com