
【题目】在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:
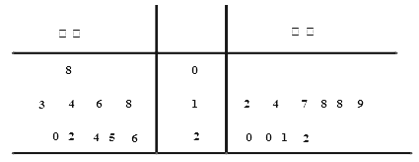
规定:当产品中的此种元素含量![]() 毫克时为优质品.
毫克时为优质品.
(1)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(2)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(1)甲厂优等品率为![]() , 乙厂优等品率为
, 乙厂优等品率为![]() .
.
(2)![]() 的分布列为
的分布列为
| 1 | 2 | 3 |
|
|
|
|
故的数学期望为![]()
【解析】
试题(1)因为通过阅读茎叶图可得到甲、乙两组测量值的数据,又因为当产品中的此种元素含量![]() 毫克时为优质品,通过数出两组优质品的数据的个数,再用优质品的的件数除以总共的样本数即可得到甲、乙的优质品率.
毫克时为优质品,通过数出两组优质品的数据的个数,再用优质品的的件数除以总共的样本数即可得到甲、乙的优质品率.
(2)因为从乙地抽出的上述10件产品中,随机抽取3件,由于乙产品中优质品有8件,所以优质品的件数共有三种情况,通过计算每种情况的概率以及数学期望的计算公式即可得到结论.
试题解析:(I)甲厂抽取的样本中优等品有7件,优等品率为![]()
乙厂抽取的样本中优等品有8件,优等品率为![]()
(II)![]() 的取值为1,2,3.
的取值为1,2,3.
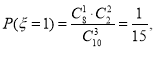
![]()
![]()
所以![]() 的分布列为
的分布列为
| 1 | 2 | 3 |
|
|
|
|
故的数学期望为![]()


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系下,已知圆O:ρ=cosθ+sinθ和直线l:![]() .
.
(1)求圆O和直线l的直角坐标方程;
(2)当θ∈(0,π)时,求直线l与圆O公共点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的发展,各种“APP”(英文单词Application的缩写,一般指手机软件)应运而生.某机构欲对A市居民手机内安装的APP的个数和用途进行调研,在使用智能手机的居民中随机抽取100人,获得了他们手机内安装APP的个数,整理得到如图所示频率分布直方图.

(Ⅰ)求a的值;
(Ⅱ)从被抽取安装APP的个数不低于50的居民中,随机抽取2人进一步调研,求这2人安装APP的个数都低于60的概率;
(Ⅲ)假设同组中的数据用该组区间的右端点值代替,以本次被抽取的居民情况为参考,试估计A市使用智能手机的居民手机内安装APP的平均个数在第几组(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,且
,且![]() 满足
满足![]() .记点
.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程,并说明是什么曲线;
的方程,并说明是什么曲线;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的动点,且直线
上的动点,且直线![]() 过点
过点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,请求出定点
?若存在,请求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
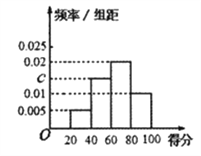
(Ⅰ)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该校安全教育活动的成效.若
的方差)来评估该校安全教育活动的成效.若![]() ,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在极坐标系中,O为极点,点![]() 在曲线
在曲线![]() 上,直线l过点
上,直线l过点![]() 且与
且与![]() 垂直,垂足为P.
垂直,垂足为P.
(1)当![]() 时,求
时,求![]() 及l的极坐标方程;
及l的极坐标方程;
(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com