
如图6所示,等边三角形OAB的边长为8 ,且其三个顶点均在抛物线E:x2=2py(p>0)上.
,且其三个顶点均在抛物线E:x2=2py(p>0)上.

图6
(1)求抛物线E的方程;
(2)设动直线l与抛物线E相切于点P,与直线y=-1相交于点Q,证明以PQ为直径的圆恒过y轴上某定点.
(1)x2=4y(2)见解析
【解析】解:(1)依题意,|OB|=8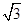 ,∠BOy=30°.
,∠BOy=30°.
设B(x,y),则x=|OB|sin30°=4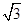 ,y=|OB|cos30°=12.
,y=|OB|cos30°=12.
因为点B(4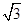 ,12)在x2=2py上,所以(4
,12)在x2=2py上,所以(4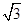 )2=2p×12,解得p=2.
)2=2p×12,解得p=2.
故抛物线E的方程为x2=4y.
(2)由(1)知y= x2,y′=
x2,y′=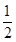 x.
x.
设P(x0,y0),则x0≠0,且l的方程为y-y0=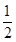 x0(x-x0),即y=
x0(x-x0),即y=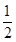 x0x-
x0x-
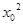 .
.
由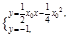 得
得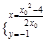
所以Q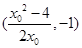 .
.
假设以PQ为直径的圆恒过定点M,由图形的对称性知M必在y轴上,设M(0,y1),令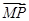 ·
·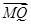 =0对满足y0=
=0对满足y0=
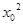 (x0≠0)的x0,y0恒成立.
(x0≠0)的x0,y0恒成立.
由于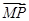 =(x0,y0-y1),
=(x0,y0-y1),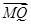 =
=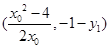 .
.
由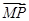 ·
·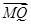 =0,得
=0,得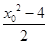 -y0-y0y1+y1+
-y0-y0y1+y1+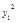 =0.
=0.
即(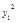 +y1-2)+(1-y1)y0=0.(*)
+y1-2)+(1-y1)y0=0.(*)
由于(*)式对满足y0=
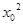 (x0≠0)的y0恒成立,所以
(x0≠0)的y0恒成立,所以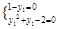
解得y1=1.
故以PQ为直径的圆恒过y轴上的定点M(0,1).


科目:高中数学 来源: 题型:
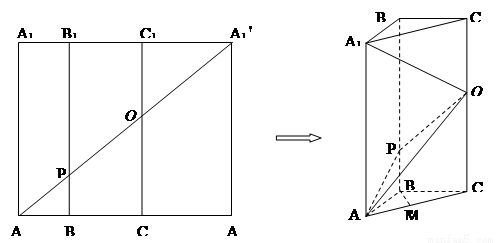
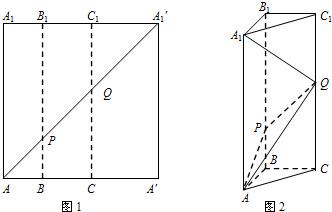 如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省郴州市高三下学期第六次月考理科数学 题型:解答题
(本小题满分13分)
如图5所示 :在边长为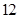 的正方形
的正方形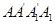 中,
中,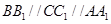 ,且
,且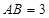 ,
,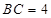 ,
,
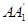 分别交
分别交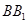 、
、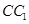 于
于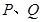 两点, 将正方形沿
两点, 将正方形沿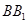 、
、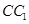 折叠,使得
折叠,使得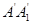 与
与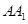 重合,
重合,
构成如图6所示的三棱柱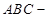
 .
.
( I )在底边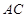 上有一点
上有一点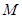 ,且
,且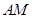 :
: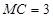 :
: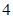 ,
求证:
,
求证: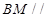 平面
平面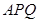 ;
;
( II )求直线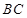 与平面
与平面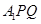 所成角的正弦值
所成角的正弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com