
【题目】若动点![]() 到定点
到定点![]() 与定直线
与定直线![]() 的距离之和为4.
的距离之和为4.
(1)求点![]() 的轨迹方程,并画出方程的曲线草图.
的轨迹方程,并画出方程的曲线草图.
(2)记(1)得到的轨迹为曲线![]() ,若曲线
,若曲线![]() 上恰有三对不同的点关于点
上恰有三对不同的点关于点![]() 对称,求
对称,求![]() 的取值范围.
的取值范围.
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
【题目】已知集合![]() 函数
函数![]() ,函数
,函数![]() 的值域为
的值域为![]() ,
,
(1)若不等式![]() 的解集为
的解集为![]() ,求
,求![]() 的值;
的值;
(2)在(1)的条件下,若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的不等式
的不等式![]() 的解集
的解集![]() ,求实数
,求实数![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减;②存在常数p,使其值域为
上单调递减;②存在常数p,使其值域为![]() ,则称函数
,则称函数![]() 为
为![]() 的“渐近函数”;
的“渐近函数”;
(1)证明:函数![]() 是函数
是函数![]()
![]() 的渐近函数,并求此时实数p的值;
的渐近函数,并求此时实数p的值;
(2)若函数![]()
![]()
![]() ,证明:当
,证明:当![]() 时,
时,![]() 不是
不是![]() 的渐近函数.
的渐近函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时参加一次数学测试,共有20道选择题,每题均有4个选项,答对得3分,答错或不答得0分,甲和乙都解答了所有的试题,经比较,他们只有2道题的选项不同,如果甲最终的得分为54分,那么乙的所有可能的得分值组成的集合为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.

(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为![]() ,观影人数记为
,观影人数记为![]() ,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后
,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后![]() 与
与![]() 的函数图象.
的函数图象.
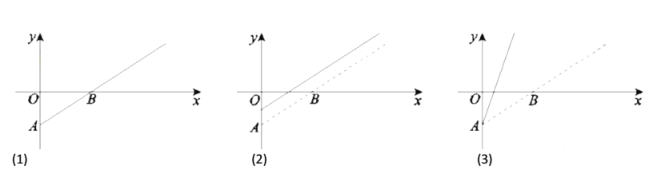
给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是____________.(填写所有正确说法的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,空间直角坐标系中,四棱锥![]() 的底面是边长为
的底面是边长为![]() 的正方形,且底面在
的正方形,且底面在![]() 平面内,点
平面内,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 平面
平面![]() ,侧棱
,侧棱![]() 与底面所成角为45°;
与底面所成角为45°;
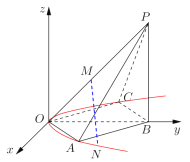
(1)若![]() 是顶点在原点,且过
是顶点在原点,且过![]() 、
、![]() 两点的抛物线上的动点,试给出
两点的抛物线上的动点,试给出![]() 与
与![]() 满足的关系式;
满足的关系式;
(2)若![]() 是棱
是棱![]() 上的一个定点,它到平面
上的一个定点,它到平面![]() 的距离为
的距离为![]() (
(![]() ),写出
),写出![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,并求
,并求![]() 的最小值;
的最小值;
(3)是否存在一个实数![]() (
(![]() ),使得当
),使得当![]() 取得最小值时,异面直线
取得最小值时,异面直线![]() 与
与![]() 互相垂直?请说明理由;
互相垂直?请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 与
与![]() 均为菱形,
均为菱形,![]() ,且
,且![]() .
.
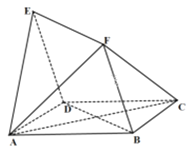
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)若![]() 为线段
为线段![]() 上的一点,满足直线
上的一点,满足直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com