练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f(x)是定义在［-1,1］上的奇函数，且f(1)=1,若m、n∈［-1,1］,m+n≠0,f ＞0，

    (1)求证：f(x)在［-1,1］上是增函数；

    (2)解不等式f(x+)＜f()；

    (3)若f(x)≤4t-3·2t+3对所有x∈［-1,1］恒成立,求实数t的取值范围.

    思路分析：(1)利用定义法证明单调性；(2)利用函数f(x)的单调性解不等式；(3)转化为求f(x)的最大值.

    (1)证明：任取-1≤x1＜x2≤1.∵f(x)为奇函数，

    ∴f(x1)-f(x2)=f(x1)+f(-x2)=·(x1-x2).

    ∵＞0,x1-x2＜0,∴f(x1)＜f(x2).

    ∴f(x)在［-1,1］上是增函数.

    (2)解：f(x+)＜f()

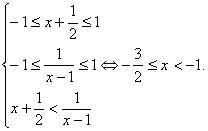
    (3)解：由(1)知f(x)在［-1,1］是增函数，且f(1)=1，

    ∴x∈［-1,1］时，f(x)≤1.

    ∵f(x)≤4t-3·2t+3对所有x∈［-1,1］恒成立，

    ∴4t-3·2t+3≥1恒成立.

    ∴(2t)2-3·2t+2≥0，

    即2t≥2或2t≤1.

    ∴t≥1或t≤0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    1
    3
    x3+
    a-3
    2
    x2+(a2-3a)x-2a    ．
    （I）如果对任意x∈[1，2]，f′（x）＞a2恒成立，求实数a的取值范围；
    （II）设函数f（x）的两个极值点分别为x1，x2判断下列三个代数式：①x1+x2+a，②
    x
    2
    1
    +
    x
    2
    2
    +a2    ，③
    x
    3
    1
    +
    x
    3
    2
    +a3
    中有几个为定值？并且是定值请求出；若不是定值，请把不是定值的表示为函数g（a），并求出g（a）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    问题1：已知函数f(x)=
    x
    1+x
    ，则f(
    1
    10
    )+f(
    1
    9
    )+    …+f(
    1
    2
    )+f(1)+f(2)+    …+f（9）+f（10）=
    19
    2
    19
    2
    ．
    我们若把每一个函数值计算出，再求和，对函数值个数较少时是常用方法，但函数值个数较多时，运算就较繁锁．观察和式，我们发现f(
    1
    2
    )+f(2)    、…、f(
    1
    9
    )+f(9)    、f(
    1
    10
    )+f(10)    可一般表示为f(
    1
    x
    )+f(x)    =
    1
    x
    1+
    1
    x
    +
    x
    1+x
    =
    1
    1+x
    +
    x
    1+x
    =
    1+x
    1+x
    =1    为定值，有此规律从而很方便求和，请求出上述结果，并用此方法求解下面问题：
    问题2：已知函数f(x)=
    1
    2x+
    		2
    ，求f（-2007）+f（-2006）+…+f（-1）+f（0）+f（1）+…+f（2007）+f（2008）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    x+1-a
    a-x
    (x≠a)
    （1）当f（x）的定义域为[a+
    1
    2
    ，a+1]    时，求f（x）的值域；
    （2）试问对定义域内的任意x，f（2a-x）+f（x）的值是否为一个定值？若是，求出这个定值；若不是，说明理由；
    （3）设函数g（x）=x2+|（x-a）f（x）|，若
    1
    2
    ≤a≤
    3
    2
    ，求g（x）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=log3
    		3
    x
    1-x
    ，M(x1，y1)，N(x2，y2)    是f（x）图象上的两点，横坐标为
    1
    2
    的点P满足2
    OP
    =
    OM
    +
    ON
    （O为坐标原点）．
    （1）求证：y1+y2为定值；
    （2）若Sn=f(
    1
    n
    )+f(
    2
    n
    )+…+f(
    n-1
    n
    )    ，其中n∈N*，n≥2令an=
    1
    6
    ，n=1
    1
    4(Sn+1)(Sn+1+1)
    ，n≥2
    ，其中n∈N*，Tn为数列{an}的前n项和，若Tn＜m（Sn+1+1）对一切n∈N*都成立，试求m的取值范围．
    （3）对于给定的实数a（a＞1）是否存在这样的数列{an}，使得f(an)=log3(
    		3
    an+1)    ，且a1=
    1
    a-1
    ？若存在，求出a满足的条件；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•嘉定区一模）（理）已知函数f(x)=log2
    		2
    x
    1-x
    ，P1（x1，y1）、P2（x2，y2）是f（x）图象上两点．
    （1）若x1+x2=1，求证：y1+y2为定值；
    （2）设Tn=f(
    1
    n
    )+f(
    2
    n
    )+…+f(
    n-1
    n
    )    ，其中n∈N*且n≥2，求Tn关于n的解析式；
    （3）对（2）中的Tn，设数列{an}满足a1=2，当n≥2时，an=4Tn+2，问是否存在角a，使不等式(1-
    1
    a1
    )(1-
    1
    a2
    )    …(1-
    1
    an
    )＜
    sinα
    		2n+1
    对一切n∈N*都成立？若存在，求出角α的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案