
【题目】在四棱锥P﹣ABCD中,PA⊥面ABCD,∠DAB=90°,AB平行于CD,AD=CD=2AB=2,E,F分别为PC,CD的中点
(1)求证:AB⊥面BEF;
(2)设PA=h,若二面角E﹣BD﹣C大于45°,求h的取值范围.
【答案】
(1)证明:以AB所在直线为x轴,以AD所在直线为y轴,
以AP所在直线为z轴建立空间直角坐标系,
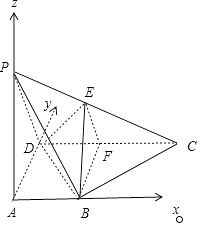
则A(0,0,0),P(0,0,h),B(1,0,0),D(0,2,0),C(2,2,0),
E(1,1, ![]() ),F(1,2,0),
),F(1,2,0),
![]() =(0,1,
=(0,1, ![]() ),
), ![]() =(0,2,0),
=(0,2,0), ![]() =(﹣2,0,0),
=(﹣2,0,0),
∴ ![]() =0,
=0, ![]() =0,
=0,
∴CD⊥BE,CD⊥BF,∴CD⊥面BEF.
∵AB平行于CD,∴AB⊥面BEF
(2)解:设面BCD的法向量为 ![]() ,则
,则 ![]() (0,0,1),
(0,0,1),
设面BDE的法向量为 ![]() (x,y,z),
(x,y,z),
∵ ![]() =(﹣1,2,0),
=(﹣1,2,0), ![]() =(0,1,
=(0,1, ![]() ),
),
∴ 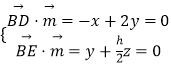 ,取x=2,得
,取x=2,得 ![]() =(2,1,﹣
=(2,1,﹣ ![]() ),
),
∵二面角E﹣BD﹣C大于45°,
∴cos< ![]() >=
>= ![]() <cos45°=
<cos45°= ![]() ,
,
由h>0,解得h> ![]() ,
,
∴h的取值范围是( ![]() ,+∞).
,+∞).
【解析】(1)以AB所在直线为x轴,以AD所在直线为y轴,以AP所在直线为z轴建立空间直角坐标系,利用向量法能证明AB⊥面BEF.(2)求出面BCD的法向量和面DE的法向量,利用向量法能求出h的取值范围.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点, ![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,85],得到的频率分布直方图如图所示.
(1)求第3,4,5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有
①刻画一组数据集中趋势的统计量有极差、方差、标准差等;刻画一组数据离散程度统计量有平均数、中位数、众数等.
②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大.
③有10个阄,其中一个代表奖品,10个人按顺序依次抓阄来决定奖品的归属,则摸奖的顺序对中奖率没有影响.
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量,![]() 获得本场比赛胜利,最终人机大战总比分定格在
获得本场比赛胜利,最终人机大战总比分定格在![]() .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
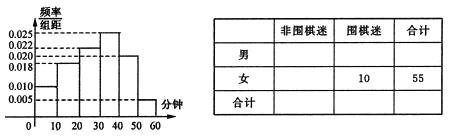
(1)根据已知条件完成如图列联表,并据此资料判断你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.010 |
| 3.74 | 6.63 |
查看答案和解析>>
科目:高中数学 来源: 题型:
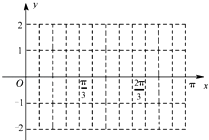
【题目】设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是 ![]() .
. 
(1)求φ;
(2)在给定的平面直角坐标系中作出该函数在x∈[0,π]的图象;
(3)求函数f(x)≥1(x∈R)的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com