
°æƒø°øŒ“–£∂‘∏þ∂˛600√˚—ß…˙Ω¯––¡À“ª¥Œ÷™ ∂≤‚ ‘,≤¢¥”÷–≥È»°¡À≤ø∑÷—ß…˙µƒ≥…º®(¬˙∑÷100∑÷)◊˜Œ™—˘±æ,ªÊ÷∆¡Àœ¬√Ê…–Œ¥ÕÍ≥…µƒ∆µ¬ ∑÷≤º±Ì∫Õ∆µ¬ ∑÷≤º÷±∑ΩÕº.
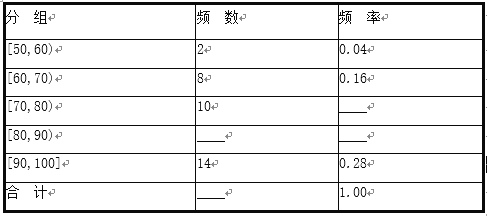
(1)ÃÓ–¥∆µ¬ ∑÷≤º±Ì÷–µƒø’∏Ò,≤π»´∆µ¬ ∑÷≤º÷±∑ΩÕº,≤¢±Í≥ˆ√ø∏ˆ–°æÿ–Œ∂‘”¶µƒ◊ð÷· ˝æð;
(2)«Îƒ„π¿À„∏√ƒÍº∂—ß…˙≥…º®µƒ÷–Œª ˝;
(3)»Áπ˚”√∑÷≤„≥È—˘µƒ∑Ω∑®¥”—˘±æ∑÷ ˝‘⁄[60,70)∫Õ[80,90)µƒ»À÷–π≤≥È»°6»À,‘Ÿ¥”6»À÷–—°2»À,«Û2»À∑÷ ˝∂º‘⁄[80,90)µƒ∏≈¬ .
°æ¥∞∏°ø(1)º˚Ω‚Œˆ£ª(2)83.125.(3)![]() .
.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫ (1)œ»ÃÓ–¥ÕÍ’˚∆µ¬ ∑÷≤º±Ì,”…¥ÀƒÐ≤π»´∆µ¬ ∑÷≤º÷±∑ΩÕº.
(2)…Ë÷–Œª ˝Œ™x,¿˚”√∆µ¬ ∑÷≤º÷±∑ΩÕº¡–≥ˆ∑Ω≥Ã,∏¯«Û≥ˆ÷–Œª ˝.
(3)”…“‚÷™—˘±æ∑÷ ˝‘⁄[60,70)”–8»À,—˘±æ∑÷ ˝‘⁄[80,90)”–16»À,”√∑÷≤„≥È—˘µƒ∑Ω∑®¥”—˘±æ∑÷ ˝‘⁄[60,70)∫Õ[80,90)µƒ»À÷–π≤≥È»°6»À,‘Ú≥È»°µƒ∑÷ ˝‘⁄[60,70)∫Õ[80,90)µƒ»À ˝∑÷±Œ™2»À∫Õ4»À.º«∑÷ ˝‘⁄[60,70)Œ™a1,a2£¨[80,90)µƒŒ™b1,b2,b3,b4.”…¥À¿˚”√¡–æŸ∑®ƒÐ«Û≥ˆ2»À∑÷ ˝∂º‘⁄[80,90)µƒ∏≈¬ .
‘Ã‚Ω‚Œˆ£∫(1)ÃÓ–¥∆µ¬ ∑÷≤º±Ì÷–µƒø’∏Ò,»Áœ¬±Ì:
∑÷°°◊È | ∆µ°° ˝ | ∆µ°°¬ |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | 0.2 |
[80,90) | 16 | 0.32 |
[90,100] | 14 | 0.28 |
∫œ°°º∆ | 50 | 1.00 |
»´∆µ¬ ∑÷≤º÷±∑ΩÕº,»Áœ¬Õº:
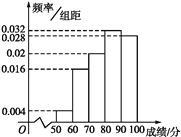
(2)…Ë÷–Œª ˝Œ™x,“¿Ã‚“‚µ√0.04+0.16+0.2+0.032°¡(x-80)=0.5,
Ω‚µ√x=83.125,À˘“‘÷–Œª ˝‘ºŒ™83.125.
(3)”…“‚÷™—˘±æ∑÷ ˝‘⁄[60,70)”–8»À,—˘±æ∑÷ ˝‘⁄[80,90)”–16»À,
”√∑÷≤„≥È—˘µƒ∑Ω∑®¥”—˘±æ∑÷ ˝‘⁄[60,70)∫Õ[80,90)µƒ»À÷–π≤≥È»°6»À,
‘Ú≥È»°µƒ∑÷ ˝‘⁄[60,70)∫Õ[80,90)µƒ»À ˝∑÷±Œ™2»À∫Õ4»À.
º«∑÷ ˝‘⁄[60,70)µƒŒ™a1,a2,‘⁄[80,90)µƒŒ™b1,b2,b3,b4.
¥”“—≥È»°µƒ6»À÷–»Œ—°¡Ω»ÀµƒÀ˘”–ø…ƒÐΩ·π˚”–15÷÷,∑÷±Œ™{a1,a2},{a1,b1},{a1,b2},{a1,b3},{a1,b4},{a2,b1},{a2,b2},{a2,b3},{a2,b4},{b1,b2},{b1,b3},{b1,b4},{b2,b3},{b2,b4},{b3,b4},
…Ë°∞2»À∑÷ ˝∂º‘⁄[80,90)°±Œ™ ¬º˛A,
‘Ú ¬º˛A∞¸¿®{b1,b2},{b1,b3},{b1,b4},{b2,b3},{b2,b4},{b3,b4}π≤6,À˘“‘P(A)=![]() .
.


 ˝—ß∞¬»¸ ÓºŸÃÏÃÏ¡∑ƒœæ©¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏
˝—ß∞¬»¸ ÓºŸÃÏÃÏ¡∑ƒœæ©¥Û—ß≥ˆ∞Ê…Áœµ¡–¥∞∏ ƒœ¥ÛΩÃ∏®«¿œ»∆≈Ð ÓºŸœŒΩ”ΩÃ≥Ü橥ۗß≥ˆ∞Ê…Áœµ¡–¥∞∏
ƒœ¥ÛΩÃ∏®«¿œ»∆≈Ð ÓºŸœŒΩ”ΩÃ≥Ü橥ۗß≥ˆ∞Ê…Áœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £¨∫Ø ˝
£¨∫Ø ˝![]() «∆Ê∫Ø ˝.
«∆Ê∫Ø ˝.
£®1£©≈–∂œ∫Ø ˝![]() µƒ∆Ê≈º–‘£¨≤¢«Û µ ˝
µƒ∆Ê≈º–‘£¨≤¢«Û µ ˝![]() µƒ÷µ;
µƒ÷µ;
£®2£©»Ù∂‘»Œ“‚µƒ![]() £¨≤ªµ» Ω
£¨≤ªµ» Ω![]() ∫„≥…¡¢£¨«Û µ ˝
∫„≥…¡¢£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß;
µƒ»°÷µ∑∂Œß;
£®3£©…Ë![]() £¨»Ù¥Ê‘⁄
£¨»Ù¥Ê‘⁄![]() £¨ π≤ªµ» Ω
£¨ π≤ªµ» Ω![]() ≥…¡¢£¨«Û µ ˝
≥…¡¢£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂‘ƒ≥–£∏þ»˝ƒÍº∂—ß…˙≤Œº”…Á«¯∑˛ŒÒ¥Œ ˝Ω¯––Õ≥º∆£¨Àʪ˙≥È»°M√˚—ß…˙◊˜Œ™—˘±æ£¨µ√µΩ’‚M√˚—ß…˙≤Œº”…Á«¯∑˛ŒÒµƒ¥Œ ˝£¨∏˘æð¥À ˝æð◊˜≥ˆ¡À∆µ ˝”Î∆µ¬ µƒÕ≥º∆±Ì∫Õ∆µ¬ ∑÷≤º÷±∑ΩÕº.
∑÷◊È | ∆µ ˝ | ∆µ¬ |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30] | 2 | 0.05 |
∫œº∆ | M | 1 |

(1)«Û≥ˆ±Ì÷–M£¨pº∞Õº÷–aµƒ÷µ£ª
(2)»Ù∏√–£∏þ»˝—ß…˙”–240»À£¨ ‘π¿º∆∏√–£∏þ»˝—ß…˙≤Œº”…Á«¯∑˛ŒÒµƒ¥Œ ˝‘⁄«¯º‰[10,15)ƒ⁄µƒ»À ˝£ª
(3)π¿º∆’‚¥Œ—ß…˙≤Œº”…Á«¯∑˛ŒÒ»À ˝µƒ÷⁄ ˝°¢÷–Œª ˝“‘º∞∆Ωæ˘ ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝∑Ω–Œ![]() ÷–£¨
÷–£¨ ![]() £¨
£¨ ![]() ”Î
”Î![]() Ωª”⁄
Ωª”⁄![]() µ„£¨œ÷Ω´
µ„£¨œ÷Ω´![]() —ÿ
—ÿ![]() ’€∆µ√µΩ»˝¿‚◊∂
’€∆µ√µΩ»˝¿‚◊∂![]() £¨
£¨ ![]() £¨
£¨ ![]() ∑÷± «
∑÷± «![]() £¨
£¨ ![]() µƒ÷–µ„.
µƒ÷–µ„.
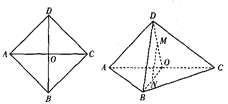
(1)«Û÷§£∫ ![]() £ª
£ª
(2)»Ù»˝¿‚◊∂![]() µƒ◊Ó¥Ûê˝Œ™
µƒ◊Ó¥Ûê˝Œ™![]() £¨µ±»˝¿‚◊∂
£¨µ±»˝¿‚◊∂![]() µƒÃª˝Œ™
µƒÃª˝Œ™![]() £¨«“
£¨«“![]() Œ™»ÒΩ« ±£¨«Û»˝¿‚◊∂
Œ™»ÒΩ« ±£¨«Û»˝¿‚◊∂![]() µƒÃª˝.
µƒÃª˝.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=lnx©Å0.5x+1£¨‘Ú≤ªµ» Ωf£®2x©Å3£©£º0.5µƒΩ‚ºØŒ™£® £©
A.{x|©Å1£ºx£º1.5}
B.{x|0.5£ºx£º2}
C.{x|x£º2}
D.{x|1.5£ºx£º2}
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=lnx£¨g£®x£©=0.5x2©Åbx£¨£®bŒ™≥£ ˝£©£Æ
£®1£©∫Ø ˝f£®x£©µƒÕºœÛ‘⁄µ„£®1£¨f£®1£©£©¥¶µƒ«–œþ”Î∫Ø ˝g£®x£©µƒÕºœÛœý«–£¨«Û µ ˝bµƒ÷µ£ª
£®2£©»Ù∫Ø ˝h£®x£©=f£®x£©+g£®x£©‘⁄∂®“”څœ≤ªµ•µ˜£¨«Û µ ˝bµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬¡–√¸Ã‚’˝»∑µƒ «£® £©
A.√¸Ã‚°∞x° R£¨ πµ√x2©Å1£º0°±µƒ∑Ò∂® «£∫x° R£¨æ˘”–x2©Å1£º0
B.√¸Ã‚°∞»Ùx=3£¨‘Úx2©Å2x©Å3=0°±µƒ∑Ò√¸Ã‚ «£∫»Ùx°Ÿ3£¨‘Úx2©Å2x©Å3°Ÿ0
C.°∞ ![]() °± «°∞
°± «°∞ ![]() °±µƒ±ÿ“™∂¯≤ª≥‰∑÷Ãıº˛
°±µƒ±ÿ“™∂¯≤ª≥‰∑÷Ãıº˛
D.√¸Ã‚°∞cosx=cosy£¨‘Úx=y°±µƒƒÊ∑Ò√¸Ã‚ «’Ê√¸Ã‚
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=x3+ax2+bx+c£¨x° [©Å2£¨2]±Ì 浃«˙œþπ˝‘≠µ„£¨«“‘⁄x=°¿1¥¶µƒ«–œþ–±¬ æ˘Œ™©Å1£¨∏¯≥ˆ“‘œ¬Ω·¬€£∫ ¢Ÿf£®x£©µƒΩ‚Œˆ ΩŒ™f£®x£©=x3©Å4x£¨x° [©Å2£¨2]£ª
¢⁄f£®x£©µƒº´÷µµ„”–«“Ωˆ”–“ª∏ˆ£ª
¢€f£®x£©µƒ◊Ó¥Û÷µ”Î◊Ó–°÷µ÷Æ∫Õµ»”⁄0£Æ
∆‰÷–’˝»∑µƒΩ·¬€”–£® £©
A.0∏ˆ
B.1∏ˆ
C.2∏ˆ
D.3∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫∫Ø ˝![]() ∂‘“ª«– µ ˝
∂‘“ª«– µ ˝![]() £¨
£¨![]() ∂º”–
∂º”–![]() ≥…¡¢£¨«“
≥…¡¢£¨«“![]() £Æ
£Æ
£®![]() £©«Û
£©«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
£®![]() £©«Û
£©«Û![]() µƒΩ‚Œˆ Ω£Æ
µƒΩ‚Œˆ Ω£Æ
£®![]() £©“—÷™
£©“—÷™![]() £¨…Ë
£¨…Ë![]() µ±
µ±![]() ±£¨≤ªµ» Ω
±£¨≤ªµ» Ω![]() ∫„≥…¡¢£¨
∫„≥…¡¢£¨ ![]() µ±
µ±![]() ±£¨
±£¨![]() «µ•µ˜∫Ø ˝£¨»Áπ˚¬˙◊„
«µ•µ˜∫Ø ˝£¨»Áπ˚¬˙◊„![]() ≥…¡¢µƒ
≥…¡¢µƒ![]() µƒºØ∫œº«Œ™
µƒºØ∫œº«Œ™![]() £¨¬˙◊„
£¨¬˙◊„![]() ≥…¡¢µƒ
≥…¡¢µƒ![]() µƒºØ∫œº«Œ™
µƒºØ∫œº«Œ™![]() £¨«Û
£¨«Û![]() £®
£®![]() Œ™»´ºØ£©£Æ
Œ™»´ºØ£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com