
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)判断函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)当![]() 时,
时,![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
科目:高中数学 来源: 题型:
【题目】【2018衡水金卷(三)】如图所示,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(I)证明: ![]() 平面
平面![]() ;
;
(II)若二面角![]() 的平面角的大小为
的平面角的大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.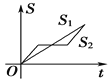 B.
B.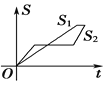 C.
C.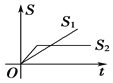 D.
D.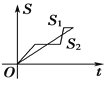
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 在倾斜角为
在倾斜角为![]() 的直线
的直线![]() 上,以坐标原点
上,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的方程为
的方程为![]() .
.
(1)写出![]() 的参数方程及
的参数方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数,
为参数, ![]() ). 以坐标原点为极点,
). 以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动点,当
上的一个动点,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线![]() 上所有的点均在直线
上所有的点均在直线![]() 的右下方,求
的右下方,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 的焦点F在直线
的焦点F在直线![]() 上。
上。
(Ⅰ)求抛物线C的方程。
(Ⅱ)过点![]() 做互相垂直的两条直线
做互相垂直的两条直线![]() 与曲线C交于A,B两点,
与曲线C交于A,B两点,![]() 与曲线C交于E,F两点,线段AB、EF的中点分别为M、N,求证:直线MN过定点P,并求出定点P的坐标。
与曲线C交于E,F两点,线段AB、EF的中点分别为M、N,求证:直线MN过定点P,并求出定点P的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元.设该公司的仪器月产量为![]() 台,当月产量不超过400台时,总收益为
台,当月产量不超过400台时,总收益为![]() 元,当月产量超过400台时,总收益为
元,当月产量超过400台时,总收益为![]() 元.(注:总收益=总成本+利润)
元.(注:总收益=总成本+利润)
(1)将利润表示为月产量![]() 的函数
的函数![]() ;
;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 图像上任意一点
图像上任意一点![]() 处的切线的斜率
处的切线的斜率![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若对于区间![]() 上任意两个不相等的实数
上任意两个不相等的实数![]() 都有
都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com