练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知双曲线方程为，问：是否存在过点M(1，1)的直线l，使得直线与双曲线交于P，Q两点，且M是线段PQ的中点？如果存在，求出直线的方程，如果不存在，请说明理由．

    【答案】不存在，见解析

    【解析】

    先考虑斜率不存在时，显然不成立，再考虑斜率存在时设l：y－1＝k(x－1)，联立双曲线方程，当判别式Δ＞0时，由根与系数的关系得x1＋x2＝,解出k,再检验即可.

    显然x＝1不满足条件，设l：y－1＝k(x－1)．

    联立y－1＝k(x－1)和，

    消去y得(2－k2)x2＋(2k2－2k)x－k2＋2k－3＝0，

    设P(x1，y1)，Q(x2，y2)，由Δ＞0，得k＜，x1＋x2＝，

    由M(1，1)为PQ的中点，得＝1，解得k＝2，这与k＜矛盾，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】命题p：α∈R，sin（π﹣α）=cosα；命题q：“0＜a＜4”是“关于x的不等式ax2+ax+1＞0的解集是实数集R”的充分必要条件，则下面结论正确的是（ ）
    A.p是假命题
    B.q是真命题
    C.“p∧q”是假命题
    D.“p∨q”是假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C的圆心在直线x﹣2y﹣3=0上，并且经过A（2，﹣3）和B（﹣2，﹣5），求圆C的标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，CA，CB分别与圆O切于A，B两点，AE是直径，OF平分∠BOE交CB的延长线于F，BD∥AC．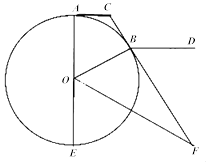

    （1）证明：OB2=BCBF；
    （2）证明：∠DBF=∠AOB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】抛物线的焦点为上任一点在轴上的射影为中点为，．

    （1）求动点的轨迹的方程；

    （2）直线过与从下到上依次交于，与交于，直线过与从下到上依次交于，与交于，，的斜率之积为，设的面积分别为，是否存在使得成等比数列？若存在，求的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，CA，CB分别与圆O切于A，B两点，AE是直径，OF平分∠BOE交CB的延长线于F，BD∥AC．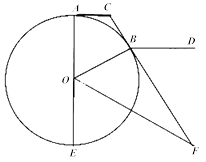

    （1）证明：OB2=BCBF；
    （2）证明：∠DBF=∠AOB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设、分别是椭圆的左、右焦点.

    （1）若是该椭圆上的一个动点，求的最大值和最小值；

    （2）设过定点的直线与椭圆交于不同的两点、，且为锐角（其中为坐标原点），求直线的斜率的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，A，B，C，D为平面四边形ABCD的四个内角．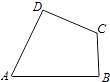

    （1）证明：tan = ；
    （2）若A+C=180°，AB=6，BC=3，CD=4，AD=5，求tan +tan +tan +tan 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的各项均为正数．若对任意的n∈N* ， 存在k∈N* ， 使得an+k2=anan+2k成立，则称数列{an}为“Jk型”数列．
    （1）若数列{an}是“J2型”数列，且a2=8，a8=1，求a2n；
    （2）若数列{an}既是“J3型”数列，又是“J4型”数列，证明：数列{an}是等比数列．

    查看答案和解析>>

    同步练习册答案