
定义一:对于一个函数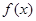 (
( ),若存在两条距离为
),若存在两条距离为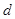 的直线
的直线 和
和 ,使得在
,使得在 时,
时, 恒成立,则称函数
恒成立,则称函数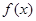 在
在
 内有一个宽度为
内有一个宽度为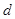 的通道。
的通道。
定义二:若一个函数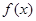 ,对于任意给定的正数
,对于任意给定的正数 ,都存在一个实数
,都存在一个实数 ,使得函数
,使得函数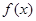 在
在 内有一个宽度为
内有一个宽度为 的通道,则称
的通道,则称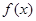 在正无穷处有永恒通道。
在正无穷处有永恒通道。
下列函数① ,②
,② ,③
,③ ,④
,④ ,
,
⑤ ,其中在正无穷处有永恒通道的函数的序号是_____________
,其中在正无穷处有永恒通道的函数的序号是_____________
②③⑤
【解析】因为①f(x)=lnx,随着x的增大,函数值也在增大,无渐近线,故不存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处无永恒通道;
② ,随着x的增大,函数值趋近于0,对于任意给定的正数ɛ,都存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处有永恒通道;
,随着x的增大,函数值趋近于0,对于任意给定的正数ɛ,都存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处有永恒通道;
③ ,随着x的增大,函数值也在增大,有两条渐近线y=±x,对于任意给定的正数ɛ,都存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处有永恒通道;
,随着x的增大,函数值也在增大,有两条渐近线y=±x,对于任意给定的正数ɛ,都存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处有永恒通道;
④f(x)=x2,随着x的增大,函数值也在增大,无渐近线,故不存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处无永恒通道;、
⑤f(x)=e-x,随着x的增大,函数值趋近于0,趋近于x轴,对于任意给定的正数ɛ,都存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ɛ的通道,故f(x)在正无穷处有永恒通道.故答案为:②③⑤


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
| sinx |
| x |
| x2-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 ,③f(x)=
,③f(x)=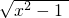 ,④f(x)=x2,⑤f(x)=e-x,
,④f(x)=x2,⑤f(x)=e-x,查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省沈阳二中高三(上)10月月考数学试卷(理科)(解析版) 题型:填空题
 ,③f(x)=
,③f(x)= ,④f(x)=x2,⑤f(x)=e-x,
,④f(x)=x2,⑤f(x)=e-x,查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省沈阳二中高三(上)10月月考数学试卷(理科)(解析版) 题型:填空题
 ,③f(x)=
,③f(x)=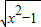 ,④f(x)=x2,⑤f(x)=e-x,
,④f(x)=x2,⑤f(x)=e-x,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com