
【题目】在约束条件  下,当t≥0时,其所表示的平面区域的面积为S(t),S(t)与t之间的函数关系用下列图象表示,正确的应该是( )
下,当t≥0时,其所表示的平面区域的面积为S(t),S(t)与t之间的函数关系用下列图象表示,正确的应该是( )
A.
B.
C.
D.
【答案】A
【解析】解:作出不等式组对应的平面区域如图,
当直线y+x=t经过C(2,0)时,此时t=2,
即当0<t≤2时,阴影部分为三角形OAB,
此时A(t,0),B(0,t),
则平面区域的面积为S(t)= ![]() t2 , 为开口向上的抛物线的一段,
t2 , 为开口向上的抛物线的一段,
当直线y+x=t经过G(0,4)时,此时t=4,
当t≥4时,对应的区域为三角形OCG,此时G(0,4),C(2,0),
此时三角形的面积为S(t)= ![]() ×2×4=4为定值,排除B,D,
×2×4=4为定值,排除B,D,
当2<t<4时,此时平面区域为四边形OCEF,
此时F(0,t),
由 ![]() 得
得 ![]() ,即E(4﹣t,2t﹣4),
,即E(4﹣t,2t﹣4),
此时四边形OCEF的面积S=S△OCG﹣S△GFE=4﹣ ![]() (4﹣t)(4﹣t)=4﹣
(4﹣t)(4﹣t)=4﹣ ![]() (t﹣4)2 , 为开口向下的抛物线,
(t﹣4)2 , 为开口向下的抛物线,
故选:A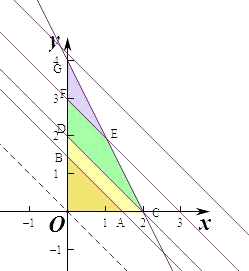


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】下列关于概率和统计的几种说法:
①10名工人某天生产同一种零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则a,b,c的大小关系为c>a>b;
②样本4,2,1,0,-2的标准差是2;
③在面积为S的△ABC内任选一点P,则随机事件“△PBC的面积小于![]() ”的概率为
”的概率为![]() ;
;
④从写有0,1,2,…,9的十张卡片中,有放回地每次抽一张,连抽两次,则两张卡片上的数字各不相同的概率是![]() .
.
其中正确说法的序号有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() 且与定直线
且与定直线![]() 相切,动圆圆心
相切,动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)已知斜率为![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,且与曲线
,且与曲线![]() 相切于点
相切于点![]() ,设
,设![]() 的中点为
的中点为![]() (其中
(其中![]() 为坐标原点).求证:直线
为坐标原点).求证:直线![]() 的斜率为0.
的斜率为0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为
的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为![]() .
.
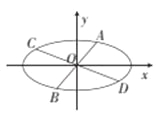
(1)若一条直径的斜率为![]() ,求该直径的共轭直径所在的直线方程;
,求该直径的共轭直径所在的直线方程;
(2)若椭圆的两条共轭直径为![]() 和
和![]() ,它们的斜率分别为
,它们的斜率分别为![]() ,证明:四边形
,证明:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 。
。
Ⅰ.求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
Ⅱ.当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
Ⅲ.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后所得函数
个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 为正三角形,平面
为正三角形,平面![]() 底面
底面![]() ,底面
,底面![]() 为梯形,
为梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.
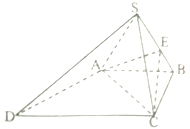
求证:(1)平面![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)e2x , g(x)=aln(x+1)+ ![]() x2+(3﹣a)x+a(a∈R).
x2+(3﹣a)x+a(a∈R).
(1)当a=9,求函数y=g(x)的单调区间;
(2)若f(x)≥g(x)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() 算得,
算得, ![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com