
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,,第五组
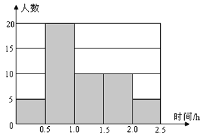
,,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.

(1)若成绩小于15秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校1800名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数和中位数.
【答案】(1)11;(2)576;(3)15.5,15.74
【解析】
试题分析:(1)根据题意,成绩在第一,二组的为良好,其频率为0.22,由频率计算公式即可算出该样本中成绩优秀的人数;(2)由频率分布直方图知成绩在第四组的频率0.32,因此估计成绩属于第三组的人数约为1800×0.32;(3)由频率分布直方图估计样本数据的中位数,众数,规律是,众数即是最高的小矩形的底边中点横坐标,中位数,出现在概率是0.5的地方
试题解析::(1)样本在这次百米测试中成绩优秀的人数0.22×50=11(人)…(2分)
(2)学校1800名学生中,成绩属于第四组的人数0.32×1800=576(人)…(2分)
(3)由图可知众数落在第三组[15,16),是15+162=15.5…(5分)
因为数据落在第一、二组的频率=1×0.06+1×0.16=0.22<0.5
数据落在第一、二、三组的频率=1×0.06+1×0.16+1×0.38=0.6>0.5…(6分)
所以中位数一定落在第三组[15,16)中.…(7分)
假设中位数是x,所以1×0.06+1×0.16+(x-15)×0.38=0.5…(9分)
解得中位数x=29919≈15.7368≈15.74…(10分)


科目:高中数学 来源: 题型:
【题目】设{an}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,a2n﹣1+a2n<0”的条件.(填“充要条件、充分不必要条件、必要不充分条件、即不充分也不必要条件”)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”。根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是 ( )
A. 甲地:总体均值为3,中位数为4
B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3
D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知cos2A+ ![]() =2cosA.
=2cosA.
(1)求角A的大小;
(2)若a=1,求△ABC的周长l的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 为两条不同的直线,
为两条不同的直线, ![]() ,
, ![]() 为两个不同的平面,对于下列四个命题:
为两个不同的平面,对于下列四个命题:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ②
②![]() ,
, ![]()
③![]() ,
, ![]() ,
, ![]() ④
④![]() ,
, ![]()
其中正确命题的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义数列![]() ,如果存在常数
,如果存在常数![]() ,使对任意正整数
,使对任意正整数![]() ,总有
,总有![]() ,那么我们称数列
,那么我们称数列![]() 为“
为“![]() —摆动数列”.
—摆动数列”.
(![]() )设
)设![]() ,
, ![]() ,
, ![]() ,判断数列
,判断数列![]() ,
, ![]() 是否为“
是否为“![]() —摆动数列”,并说明理由;
—摆动数列”,并说明理由;
(2)已知“![]() —摆动数列”
—摆动数列”![]() 满足:
满足: ![]() ,求常数
,求常数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosxsin(x+![]() )﹣
)﹣![]() cos2x+
cos2x+![]() ,x∈R.
,x∈R.
(1)求f(x)的单调递增区间;
(2)在锐角△ABC中,角A,B,C的对边分别a,b,c,若f(A)=![]() ,a=
,a=![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com