
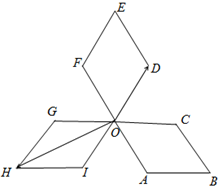
 如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}=x\overrightarrow{OD}+y\overrightarrow{OH}$,则x+y的最大值为4.
如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}=x\overrightarrow{OD}+y\overrightarrow{OH}$,则x+y的最大值为4. 分析 由条件可以看出G,O,C三点共线,并且OE的连线垂直于GC,从而可以分别以OC,OE两直线为x,y轴,建立平面直角坐标系,可以确定D,H的坐标:D($1,\sqrt{3}$),H($-3,-\sqrt{3}$),可设P(X,Y).从而可根据条件$\overrightarrow{OP}=x\overrightarrow{OD}+y\overrightarrow{OH}$,用X,Y表示出x,y,并且可以得到x+y=$-X+\frac{2\sqrt{3}}{3}Y$,可设x+y=z,从而可以得到$Y=\frac{\sqrt{3}}{2}X+\frac{\sqrt{3}}{2}z$,该方程表示的直线的截距为$\frac{\sqrt{3}}{2}z$,可以看出截距最大时,z最大,并且根据图形可以看出当直线过E点时截距最大,这样求出点E的坐标带入直线方程即可求出z,即求出x+y的最大值.
解答 解:根据条件知,G,O,C三点共线,连接OE,则OE⊥GC;
∴分别以OC,OE所在直线为x轴,y轴,建立如图所示平面直角坐标系,设棱形的边长为2,则: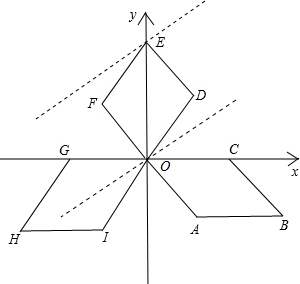
D(1,$\sqrt{3}$),H(-3,$-\sqrt{3}$);
设P(X,Y),则:$(X,Y)=x(1,\sqrt{3})+y(-3,-\sqrt{3})$;
∴$\left\{\begin{array}{l}{X=x-3y}\\{Y=\sqrt{3}x-\sqrt{3}y}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=-\frac{1}{2}X+\frac{\sqrt{3}}{2}Y}\\{y=-\frac{1}{2}X+\frac{\sqrt{3}}{6}Y}\end{array}\right.$;
∴$x+y=-X+\frac{2\sqrt{3}}{3}Y$;
设x+y=z,则:$Y=\frac{\sqrt{3}}{2}X+\frac{\sqrt{3}}{2}z$,$\frac{\sqrt{3}}{2}z$表示在y轴上的截距;
当截距最大时,z取到最大值;
由图形可以看出当直线经过点E($0,2\sqrt{3}$)时截距最大;
∴$2\sqrt{3}=0+\frac{\sqrt{3}}{2}z$;
∴z=4;
∴x+y的最大值为4.
故选:B.
点评 考查通过建立平面直角坐标系,利用向量坐标解决向量问题的方法,能确定平面上点的坐标,以及向量坐标的加法和数乘运算,直线的点斜式方程,线性规划的运用.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,\frac{1}{2}})$ | B. | $({0,\frac{1}{2}})$ | C. | $({\frac{1}{2},+∞})$ | D. | $({0,\frac{1}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x>1,则x2+x≤2 | B. | 若x2+x≤2,则x≤1 | C. | 若x2+x>2,则x>1 | D. | 若x≤1,则x2+x≤2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com