
【题目】已知中心在原点的双曲线C的右焦点为(2,0),右顶点为( ![]() ,0)
,0)
(1)求双曲线C的方程;
(2)若直线l:y=kx+ ![]() 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 ![]() >2(其中O为原点).求k的取值范围.
>2(其中O为原点).求k的取值范围.
【答案】
(1)解:设双曲线方程为 ![]() (a>0,b>0).
(a>0,b>0).
由已知得 ![]() .
.
故双曲线C的方程为 ![]() .
.
(2)解:将 ![]()
![]() .
.
由直线l与双曲线交于不同的两点得 ![]()
即 ![]() .①
.①
设A(xA,yA),B(xB,yB),
则 ![]() ,
,
而 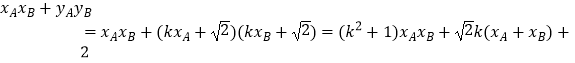 =
= ![]() .
.
于是 ![]()
![]() .②
.②
由①、②得 ![]() .
.
故k的取值范围为 ![]() .
.
【解析】(1)由双曲线的右焦点与右顶点易知其标准方程中的c、a,进而求得b,则双曲线标准方程即得;(2)首先把直线方程与双曲线方程联立方程组,然后消y得x的方程,由于直线与双曲线恒有两个不同的交点,则关于x的方程必为一元二次方程且判别式大于零,由此求出k的一个取值范围;再根据一元二次方程根与系数的关系用k的代数式表示出xA+xB , xAxB , 进而把条件 ![]() >2转化为k的不等式,又求出k的一个取值范围,最后求k的交集即可.
>2转化为k的不等式,又求出k的一个取值范围,最后求k的交集即可.


 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且R(x)=  .
.
(1)求年利润W(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (其中常数a>0,且a≠1).
(其中常数a>0,且a≠1).
(1)当a=10时,解关于x的方程f(x)=m(其中常数m>2 ![]() );
);
(2)若函数f(x)在(﹣∞,2]上的最小值是一个与a无关的常数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={y|y=x2﹣2x﹣3,x∈R},B={x|log2x<﹣1},C={k|函数f(x)= ![]() 在(0,+∞)上是增函数}.
在(0,+∞)上是增函数}.
(1)求A,B,C;
(2)求A∩C,(UB)∪C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数fk(x)=2x﹣(k﹣1)2﹣x(k∈Z),x∈R,g(x)= ![]() .
.
(1)若f2(x)=2,求x的值.
(2)判断并证明函数y=g(x)的单调性;
(3)若函数y=f0(2x)+2mf2(x)在x∈[1,+∞)上有零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为
=1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为 ![]() .以原点为圆心,椭圆的短轴长为直径的圆与直线x﹣y+
.以原点为圆心,椭圆的短轴长为直径的圆与直线x﹣y+ ![]() =0相切.
=0相切. 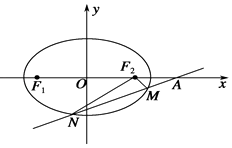
(1)求椭圆C的方程;
(2)如图,若斜率为k(k≠0)的直线l与x轴、椭圆C顺次相交于A,M,N(A点在椭圆右顶点的右侧),且∠NF2F1=∠MF2A.求证直线l恒过定点,并求出斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx,g(x)=x3+ax2﹣x+2 (Ⅰ)如果函数g(x)的单调递减区间为(﹣ ![]() ,1),求函数g(x)的解析式;
,1),求函数g(x)的解析式;
(Ⅱ)对一切的x∈(0,+∞),2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com