
【题目】双曲线![]() :
:![]() 的左右顶点分别为
的左右顶点分别为![]() ,
,![]() ,动直线
,动直线![]() 垂直
垂直![]() 的实轴,且交
的实轴,且交![]() 于不同的两点
于不同的两点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 的两条互相垂直的弦
的两条互相垂直的弦![]() ,
,![]() ,证明:过两弦
,证明:过两弦![]() ,
,![]() 中点的直线恒过定点.
中点的直线恒过定点.
科目:高中数学 来源: 题型:
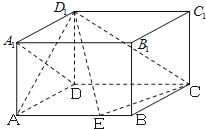
【题目】已知在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(Ⅰ)求证:D1E⊥A1D;
(Ⅱ)在棱AB上是否存在点E使得AD1与平面D1EC成的角为![]() ?若存在,求出AE的长,若不存在,说明理由.
?若存在,求出AE的长,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,若正整数
,若正整数![]() ,使得当
,使得当![]() 时,有
时,有![]() ,则称
,则称![]() 为“
为“![]() 不减数列”.
不减数列”.
(1)设![]() ,
,![]() 均为正整数,且
均为正整数,且![]() ,甲:
,甲:![]() 为“
为“![]() 不减数列”,乙:
不减数列”,乙:![]() 为“
为“![]() 不减数列”.试判断命题:“甲是乙的充分条件”的真假,并说明理由;
不减数列”.试判断命题:“甲是乙的充分条件”的真假,并说明理由;
(2)已知函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称,数列
对称,数列![]() 满足
满足![]() ,
,![]() ,如果
,如果![]() 为“
为“![]() 不减数列”,试求
不减数列”,试求![]() 的最小值;
的最小值;
(3)对于(2)中的![]() ,设
,设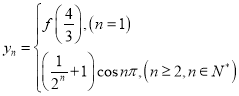 ,且
,且![]() .是否存在实数
.是否存在实数![]() 使得
使得![]() 为“
为“![]() 不减数列”?若存在,求出
不减数列”?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是古希腊数学家阿基米德用平衡法求球的体积所用的图形.此图由正方形![]() 、半径为
、半径为![]() 的圆及等腰直角三角形构成,其中圆内切于正方形,等腰三角形的直角顶点与
的圆及等腰直角三角形构成,其中圆内切于正方形,等腰三角形的直角顶点与![]() 的中点
的中点![]() 重合,斜边在直线
重合,斜边在直线![]() 上.已知
上.已知![]() 为
为![]() 的中点,现将该图形绕直线
的中点,现将该图形绕直线![]() 旋转一周,则阴影部分旋转后形成的几何体积为( )
旋转一周,则阴影部分旋转后形成的几何体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Serum Drug Concentration)是指药物吸收后在血浆内的总浓度(单位:mg/ml),通常用血药浓度来研究药物的作用强度.下图为服用同等剂量的三种新药后血药浓度的变化情况,其中点![]() 的横坐标表示服用第
的横坐标表示服用第![]() 种药后血药浓度达到峰值时所用的时间,其它点的横坐标分别表示服用三种新药后血药浓度第二次达到峰值一半时所用的时间(单位:h),点
种药后血药浓度达到峰值时所用的时间,其它点的横坐标分别表示服用三种新药后血药浓度第二次达到峰值一半时所用的时间(单位:h),点![]() 的纵坐标表示第
的纵坐标表示第![]() 种药的血药浓度的峰值.(
种药的血药浓度的峰值.(![]() )
)

①记![]() 为服用第
为服用第![]() 种药后达到血药浓度峰值时,血药浓度提高的平均速度,则
种药后达到血药浓度峰值时,血药浓度提高的平均速度,则![]() 中最大的是_______;
中最大的是_______;
②记![]() 为服用第
为服用第![]() 种药后血药浓度从峰值降到峰值的一半所用的时间,则
种药后血药浓度从峰值降到峰值的一半所用的时间,则![]() 中最大的是_______
中最大的是_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( ).
A.“![]() ,
,![]() 互为共轭复数”是“
互为共轭复数”是“![]() ”的充分不必要条件
”的充分不必要条件
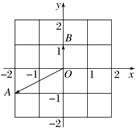
B.如图,在复平面内,若复数![]() ,
,![]() 对应的向量分别是
对应的向量分别是![]() ,
,![]() ,则复数
,则复数![]() 对应的点的坐标为
对应的点的坐标为![]()
C.若函数![]() 恰在
恰在![]() 上单调递减,则实数
上单调递减,则实数![]() 的值为4
的值为4
D.函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com