
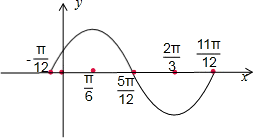
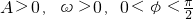 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为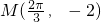 .
.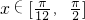 ,求f(x)的值域.
,求f(x)的值域.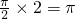 ,A=2,ω=
,A=2,ω=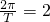 ,
,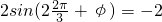 ,∴φ=
,∴φ= +2kπ,k∈Z,∵
+2kπ,k∈Z,∵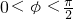

 ).
). ).
).
 ,得到函数y=sin(x+
,得到函数y=sin(x+ )
) 倍,纵坐标不变得到函数y=sin(2x+
倍,纵坐标不变得到函数y=sin(2x+ )
) ).
). ,2kπ-
,2kπ- ],
], ≤2x+
≤2x+ ≤-
≤- +2kπ,
+2kπ, ≤x≤kπ-
≤x≤kπ- ,k∈Z;
,k∈Z;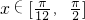 ,2x+
,2x+ ∈
∈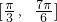 ,2sin(2x+
,2sin(2x+ )∈[-1,2],所以f(x)的值域为:[-1,2].
)∈[-1,2],所以f(x)的值域为:[-1,2]. 属于这个区间列出关于x的不等式,再由x的范围求出不等式的解集,即为函数的单调递减区间.
属于这个区间列出关于x的不等式,再由x的范围求出不等式的解集,即为函数的单调递减区间. 的范围,然后求出函数值的范围.
的范围,然后求出函数值的范围.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com