
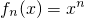 ,n∈N*,其导函数记为f′n(x),且满足.
,n∈N*,其导函数记为f′n(x),且满足. 在区间(0,1)上的实数根的个数.
在区间(0,1)上的实数根的个数. ,x3=1,且x1<x2<x3,
,x3=1,且x1<x2<x3,| x | (-∞,0) | 0 | (0, ) ) |  | ( ,1) ,1) | (1,+∞) | |
| y′ | + | 0 | + | 0 | - | 0 | + |
| y | 极大值 | 极小值 |
 时,y极大=
时,y极大= ;当x=1时,y极小=0.
;当x=1时,y极小=0.| x | (-∞,0) | 0 | (0, ) ) |  | ( ,1) ,1) | (1,+∞) | |
| y′ | + | 0 | + | 0 | - | 0 | + |
| y | 极大值 |
 时,y极大=
时,y极大= ;无极小值.
;无极小值. =
=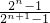 ,即
,即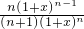 =
=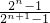 (x≠-1),
(x≠-1),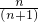 •
• =
=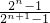 (x≠-1),
(x≠-1),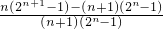 =
=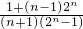 >0,
>0,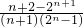 ,而对于n∈N*,有2n+1>n+2(利用二项式定理可证),
,而对于n∈N*,有2n+1>n+2(利用二项式定理可证), ,x3=1,且x1<x2<x3,分n为正偶数与n为正奇数讨论,随x的变化,y′与y的变化情况即可求g(x)的极大值与极小值;
,x3=1,且x1<x2<x3,分n为正偶数与n为正奇数讨论,随x的变化,y′与y的变化情况即可求g(x)的极大值与极小值;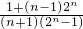 >0,对于n∈N*,有2n+1>n+2,于是x-1=
>0,对于n∈N*,有2n+1>n+2,于是x-1=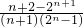 <0,从而可求得0<x<1,于是在区间(0,1)上方程只有唯一实根.
<0,从而可求得0<x<1,于是在区间(0,1)上方程只有唯一实根.

 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f2(x2)-f2(x1) | x2-x1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com