
设函数 是定义在
是定义在 上的周期为2的偶函数,当
上的周期为2的偶函数,当 时,
时,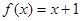 ,则
,则 =___________.
=___________.
科目:高中数学 来源: 题型:填空题
关于函数f(x)=4sin(2x+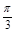 )(x∈R),有下列命题:
)(x∈R),有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是 的整数倍;
的整数倍;
②y= f(x)的表达式可改写为y=4cos(2x- );
);
③y= f(x)的图象关于点(- ,0)对称;
,0)对称;
④y= f(x)的图象关于直线x=- 对称.
对称.
其中正确的命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com