
【题目】2020年是我国打赢脱贫攻坚战收官之年,为落实“精准扶贫”政策,某扶贫小组为一“对点帮扶”农户引种了一种新的经济农作物,并指导该农户于2020年初开始种植.已知该经济农作物每年每亩的种植成本为1000元,根据前期各方面调查发现,该经济农作物的市场价格和亩产量均具有随机性,且两者互不影响,其具体情况如下表:
该经济农作物亩产量 | 900 | 1200 | 该经济农作物市场价格(元 | 15 | 20 | |
概率 |
|
| 概率 |
|
|
(1)设2020年该农户种植该经济农作物一亩的纯收入为![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)若该农户从2020年开始,连续三年种植该经济农作物,假设三年内各方面条件基本不变,求这三年中该农户种植该经济农作物一亩至少有两年的纯收入不少于16000元的概率;
(3)2020年全国脱贫标准约为人均纯收入4000元.假设该农户是一个四口之家,且该农户在2020年的其他方面的支出与收入正好相抵,能否凭这一亩经济农作物的纯收入,预测该农户在2020年底可以脱贫?并说明理由.
【答案】(1)答案见解析;(2)![]() ;(3)能预测该农户在2020年底可以脱贫;答案见解析.
;(3)能预测该农户在2020年底可以脱贫;答案见解析.
【解析】
(1)首先由题意假设出事件A,B,并确定出发生的概率,因为利润=产量![]() 市场价格
市场价格![]() 成本,
成本,
进而得到![]() 所有可能的取值,再由概率的基本性质可得相应概率,得到
所有可能的取值,再由概率的基本性质可得相应概率,得到![]() 的分布列
的分布列
(2)将所求概率的事件记为C,由题意知每年收入相互独立,再由概率的基本性质可得![]() ,设这三年中有
,设这三年中有![]() 年的纯收入不少于16000元,变量
年的纯收入不少于16000元,变量![]() 服从二项分布,即可求解.
服从二项分布,即可求解.
(3)由(1)计算![]() ,再与4000进行比较即可求解.
,再与4000进行比较即可求解.
(1)由题意知:
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以![]() 的所有可能取值为:23000,17000,12500.
的所有可能取值为:23000,17000,12500.
设![]() 表示事件“作物产量为
表示事件“作物产量为![]() ”,则
”,则![]() ;
;
![]() 表示事件“作物市场价格为15元
表示事件“作物市场价格为15元![]() ”,则
”,则![]() .
.
则:![]() ,
,
![]() ,
,
![]() ,
,
所以![]() 的分布列为:
的分布列为:
| 23000 | 17000 | 12500 |
|
|
|
|
(2)设![]() 表示事件“种植该农作物一亩一年的纯收入不少于16000元”,
表示事件“种植该农作物一亩一年的纯收入不少于16000元”,
则![]() ,
,
设这三年中有![]() 年的纯收入不少于16000元,
年的纯收入不少于16000元,
则有:![]() ,
,
所以这三年中至少有两年的纯收入不少于16000元的概率为
![]() .
.
(3)由(1)知,2020年该农户种植该经济农作物一亩的预计纯收入为
![]() (元),
(元),
![]() ,
,
凭这一亩经济农作物的纯收入,该农户的人均纯收入超过了国家脱贫标准,
所以,能预测该农户在2020年底可以脱贫.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,因此被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”的一个示意图,整个图形是一个圆面,其中黑色区域在![]() 轴右侧部分的边界为一个半圆.给出以下命题:
轴右侧部分的边界为一个半圆.给出以下命题:
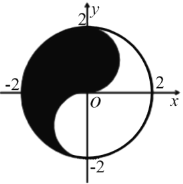
①在太极图中随机取一点,此点取自黑色部分的概率是![]() ;
;
②当![]() 时,直线
时,直线![]() 与白色部分有公共点;
与白色部分有公共点;
③黑色阴影部分中一点![]() ,则
,则![]() 的最大值为2;
的最大值为2;
④设点![]() ,点
,点![]() 在此太极图上,使得
在此太极图上,使得![]() ,
,![]() 的范围是
的范围是![]() .
.
其中所有正确结论的序号是( )
A.①②B.②③C.①③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三十二班同学设计了一个如图所示的“蝴蝶形图案”(阴影区域)来预示在6月的高考中,同学们展翅高飞,其中![]() 是过抛物线
是过抛物线![]() 的焦点
的焦点![]() 的两条弦,且
的两条弦,且![]() ,点
,点![]() 为
为![]() 轴上一点,记
轴上一点,记![]() ,其中
,其中![]() 为锐角.
为锐角.
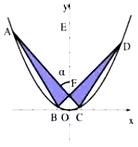
(1)求抛物线的方程;
(2)当“蝴蝶形图案”的面积最小时,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,P为直线
中,P为直线![]() :
:![]() 上的动点,动点Q满足
上的动点,动点Q满足![]() ,且原点O在以
,且原点O在以![]() 为直径的圆上.记动点Q的轨迹为曲线C
为直径的圆上.记动点Q的轨迹为曲线C
(1)求曲线C的方程:
(2)过点![]() 的直线
的直线![]() 与曲线C交于A,B两点,点D(异于A,B)在C上,直线
与曲线C交于A,B两点,点D(异于A,B)在C上,直线![]() ,
,![]() 分别与x轴交于点M,N,且
分别与x轴交于点M,N,且![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com