
分析 (Ⅰ)利用an=a1+(a2-a1)+(a3-a2)+…+(an-an-1),及其等差数列的求和公式即可得出.
(Ⅱ)由${b_n}=\frac{n(n+1)}{{n×{4^n}}}=\frac{n+1}{4^n}$,利用“错位相减法”、等比数列的求和公式及其数列的单调性即可得出.
解答 (Ⅰ)解:an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=$1+2+3+…+n=\frac{n(n+1)}{2}$.
(Ⅱ)证明:${b_n}=\frac{n(n+1)}{{n×{4^n}}}=\frac{n+1}{4^n}$,
其前n项和Tn=$\frac{2}{4}$+$\frac{3}{{4}^{2}}$+…+$\frac{n+1}{{4}^{n}}$,
$\frac{1}{4}$Tn=$\frac{2}{{4}^{2}}$+$\frac{3}{{4}^{3}}$+…+$\frac{n}{{4}^{n}}$+$\frac{n+1}{{4}^{n+1}}$,
∴$\frac{3}{4}$Tn=$\frac{2}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+…+$\frac{1}{{4}^{n}}$-$\frac{n+1}{{4}^{n+1}}$,
=$\frac{1}{4}$+$\frac{\frac{1}{4}(1-\frac{1}{{4}^{n}})}{1-\frac{1}{4}}$-$\frac{n+1}{{4}^{n+1}}$=$\frac{7}{12}$-$\frac{3n+7}{3×{4}^{n+1}}$,
∴Tn=$\frac{7}{9}$-$\frac{3n+7}{9×{4}^{n}}$<$\frac{7}{9}$.
点评 本题考查了“错位相减法”、等差数列与等比数列的求和公式及其数列的单调性,考查了推理能力与计算能力,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | -$\frac{5}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
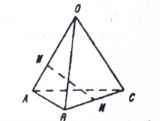
如图,空间四边形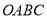 中,
中,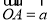 ,
,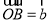 ,
,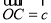 ,点
,点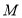 在
在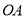 上,且
上,且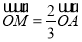 ,点
,点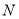 为
为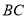 中点,则
中点,则 等于( )
等于( )
A.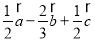 B.
B.
C.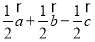 D.
D.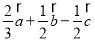
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 0.9 | 1.9 | 3.2 | 4.4 |
| A. | 0.6 | B. | 0.7 | C. | 0.8 | D. | 0.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com