
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过4(尾/立方米)时,
不超过4(尾/立方米)时,![]() 的值为
的值为![]() (千克/年);当
(千克/年);当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 达到
达到![]() (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因,![]() 的值为
的值为![]() (千克/年).
(千克/年).
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当养殖密度![]() 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)![]() 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
科目:高中数学 来源: 题型:
【题目】我国古代数学家刘徽是公元三世纪世界上最杰出的数学家,他在《九章算术圆田术》注中,用割圆术证明了圆面积的精确公式,并给出了计算圆周率的科学方法.所谓“割圆术”,即通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率(圆周率指圆周长与该圆直径的比率).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径![]()
,此时圆内接正六边形的周长为![]()
,此时若将圆内接正六边形的周长等同于圆的周长,可得圆周率为3,当用正二十四边形内接于圆时,按照上述算法,可得圆周率为__________.(参考数据: ![]()
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与
与![]() (
(![]() 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为![]() .若动点
.若动点![]() 满足
满足![]() ,试探究是否存在两个定点
,试探究是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy上取两个定点![]() 再取两个动点
再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求直线![]() 与
与![]() 交点M的轨迹C的方程;
交点M的轨迹C的方程;
(Ⅱ)过![]() 的直线与轨迹C交于P,Q,过P作
的直线与轨迹C交于P,Q,过P作![]() 轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若
轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活经验告诉我们,当水注进容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在下图中请选择与容器相匹配的图像,A对应________;B对应________;C对应________;D对应________.
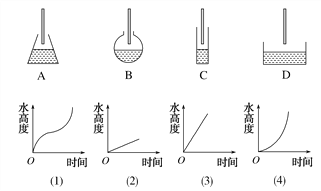
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(![]() ,简称
,简称![]() )是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为
)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为![]() 等六项.空气质量按照
等六项.空气质量按照![]() 大小分为六级:一级
大小分为六级:一级![]() 为优;二级
为优;二级![]() 为良好;三级
为良好;三级![]() 为轻度污染;四级
为轻度污染;四级![]() 为中度污染;五级
为中度污染;五级![]() 为重度污染;六级
为重度污染;六级![]() 为严重污染.
为严重污染.
某人根据环境监测总站公布的数据记录了某地某月连续10天![]() 的茎叶图如图所示:
的茎叶图如图所示:

(1)利用访样本估计该地本月空气质量优良(![]() )的天数;(按这个月总共30天计算);
)的天数;(按这个月总共30天计算);
(2)若从样本中的空气质量不佳(![]() )的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
)的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=3,AD=4.现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
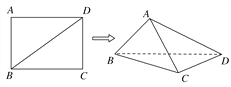
(1)试问:在折叠的过程中,直线AB与CD能否垂直?若能,求出相应a的值;若不能,请说明理由;
(2)求四面体A-BCD体积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com