
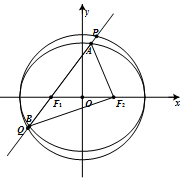
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=a2,F1(-1,0),F2(1,0)分别是椭圆的左、右两焦点,过F1且倾斜角为α$({α∈({0,\frac{π}{2}}]})$的动直线l交椭圆C于A,B两点,交圆O于P,Q两点(如图所示,点A在x轴上方).当α=$\frac{π}{4}$时,弦PQ的长为$\sqrt{14}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=a2,F1(-1,0),F2(1,0)分别是椭圆的左、右两焦点,过F1且倾斜角为α$({α∈({0,\frac{π}{2}}]})$的动直线l交椭圆C于A,B两点,交圆O于P,Q两点(如图所示,点A在x轴上方).当α=$\frac{π}{4}$时,弦PQ的长为$\sqrt{14}$. 分析 (1)取PQ的中点D,连接OD,OP,求出OD,利用弦PQ的长为$\sqrt{14}$,求出OQ,可得a,结合隐含条件求得b,则圆O和椭圆C的方程可求;
(2)由(1)可得椭圆的长半轴长及离心率,设B的坐标,利用焦半径公式可得|BF2|,|AF2|,代入2|BF2|=|AF2|+|AB|,求出B的坐标,由直线方程的两点式求得B、F1所在直线方程,即直线PQ的方程.
解答 解:(1)取PQ的中点D,连接OD,OP,
由$α=\frac{π}{4}$,c=1,可得OD=$\frac{\sqrt{2}}{2}$,
∵弦PQ的长为$\sqrt{14}$,
∴$O{Q}^{2}=\frac{P{Q}^{2}}{4}$+OD2=4,
∴a2=4,b2=a2-c2=3,
∴圆O的方程为x2+y2=4,
椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)由(1)知,a=2,e=$\frac{1}{2}$,
又2|BF2|=|AF2|+|AB|,得2|BF2|=|AF2|+|AF1|+|BF1|,
∴2|BF2|=4+|BF1|,
设B(x0,y0),则|BF2|=$2-\frac{1}{2}{x}_{0}$,|BF1|=$2+\frac{1}{2}{x}_{0}$,
代入2|BF2|=4+|BF1|,得$2(2-\frac{1}{2}{x}_{0})=4+2+\frac{1}{2}{x}_{0}$,解得${x}_{0}=-\frac{4}{3}$,
代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,得${y}_{0}=-\frac{\sqrt{15}}{3}$.
∴B($-\frac{4}{3},-\frac{\sqrt{15}}{3}$),
则直线PQ的方程为:$\frac{y}{-\frac{\sqrt{15}}{3}}=\frac{x+1}{-\frac{4}{3}+1}$,即$\sqrt{15}x-y+\sqrt{15}=0$.
点评 本题考查圆和椭圆的方程,考查等差数列的性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | sin1 | B. | cos1 | C. | 2sin1 | D. | 2cos1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥S-ABC中,AS=AB,CS=CB,点E,F,G分别是棱SA,SB,SC的中点.求证:
如图,在三棱锥S-ABC中,AS=AB,CS=CB,点E,F,G分别是棱SA,SB,SC的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 7 | C. | 17 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底面 ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底面 ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com