
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,点
,点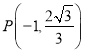 在椭圆
在椭圆![]() 上,
上, ![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 分别交于
分别交于![]() 两点.
两点.
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)若![]() 的面积为
的面积为![]() 为坐标原点,求直线
为坐标原点,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() 与
与![]() 的等差中项为
的等差中项为![]() (
(![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() ,是不等式
,是不等式![]() (
(![]() )恒成立,若存在,求出
)恒成立,若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
(3)设
![]() ,若集合
,若集合![]() 恰有
恰有![]() 个元素,求实数
个元素,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=![]() .
.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A﹣BE﹣P的大小.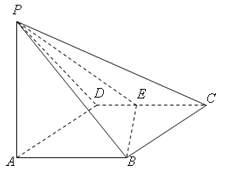
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1= ![]() ,
, 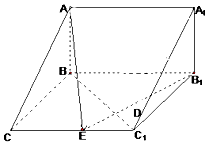
(1)试在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1;
(2)在(1)的条件下,求AE和BC1所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=![]() (万元).当年产量不小于80千件时,C(x)=51x+
(万元).当年产量不小于80千件时,C(x)=51x+![]() (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
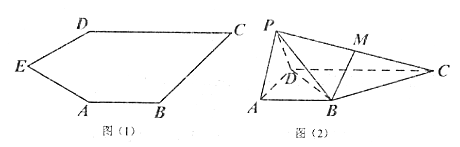
【题目】如图(1)五边形![]() 中,
中, ![]()
![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() ,如图(2),点
,如图(2),点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若四棱柱![]() 的体积为
的体积为![]() ,求四面体
,求四面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为R,集合A={x||x|≤2},B={x| ![]() >0},则A∩RB=( )
>0},则A∩RB=( )
A.[﹣2,1)
B.[﹣2,1]
C.[﹣2,2]
D.[﹣2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com