
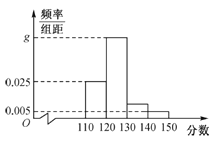
【题目】某重点中学高三的一名学生在高考前对他在高三近一年中的所有数学考试(含模拟考试、月考、平时训练等各种类型的试卷)分数进行统计,以此来估计自己在高考中的大致分数.为此,随机抽取了若干份试卷作为样本,根据此样本数据作出如下频率分布统计表和频率分布直方图.
分组 | 频数 | 频率 |
| 20 | 0.25 |
| 50 |
|
|
|
|
| 4 | 0.05 |
(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值;
的值;
(2)若同组中的每个数据用该组区间的中点值代替,试根据频率分布直方图求该学生高三年级数学考试分数的中位数和平均数,并对该学生自己在高考中的数学成绩进行预测.
【答案】(1)![]() ;
;![]() ;
;![]() ;
;![]() (2)平均数为124.25;中位数为124;预测该学生自己在高考中的大致分数大致在124分左右.
(2)平均数为124.25;中位数为124;预测该学生自己在高考中的大致分数大致在124分左右.
【解析】
![]() 根据频率分布表求出样本容量,进而求出
根据频率分布表求出样本容量,进而求出![]() 的值,结合频率分布直方图求出
的值,结合频率分布直方图求出![]() 即可;
即可;
![]() 利用频率分布直方图代入平均数公式求解,根据频率分布直方图,可知中位数位于区间
利用频率分布直方图代入平均数公式求解,根据频率分布直方图,可知中位数位于区间![]() ,设中位数为
,设中位数为![]() ,代入中位数公式求出
,代入中位数公式求出![]() 即可.
即可.
![]() 由题意知,样本容量为
由题意知,样本容量为![]() ,
,
根据频率分布表可知,![]() ,
,
根据“频率等于频数除以样本容量”得,![]() ,
,
![]() ,
,
根据频率分布直方图可知,![]() .
.
(2)由(1)得,频率分布统计表如下:
分组 | 频数 | 频率 |
| 20 | 0.25 |
| 50 | 0.625 |
| 6 | 0.075 |
| 4 | 0.05 |
合计 | 80 | 1 |
根据频率分布直方图估计该学生高三年级数学考试分数的平均数为
![]() ,
,
根据频率分布直方图,可知中位数位于区间![]() 内,
内,
所以设该学生高三年级模拟考试分数的中位数为![]() ,
,
则![]() ,解得
,解得![]() ,
,
所以该学生高三年级模拟考试分数的中位数为124,
因此预测该学生自己在高考中的大致分数大致在124分左右.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 上顶点为
上顶点为![]() ,右顶点为
,右顶点为![]() ,离心率
,离心率![]() ,圆
,圆![]() :
:![]() 与直线
与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的三个动点,直线
上的三个动点,直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() .
.
(i)若![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(ii)若![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十四届全国冬季运动会召开期间,某校举行了“冰上运动知识竞赛”,为了解本次竞赛成绩情况,从中随机抽取部分学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
(1)求![]() 、
、![]() 、
、![]() 的值及随机抽取一考生其成绩不低于70分的概率;
的值及随机抽取一考生其成绩不低于70分的概率;
(2)若从成绩较好的3、4、5组中按分层抽样的方法抽取5人参加“普及冰雪知识”志愿活动,并指定2名负责人,求从第4组抽取的学生中至少有一名是负责人的概率.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 15 | 0.15 |
第2组 |
| 35 | 0.35 |
第3组 |
| b | 0.20 |
第4组 |
| 20 |
|
第5组 |
| 10 | 0.1 |
合计 |
| 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司年会举行抽奖活动,每位员工均有一次抽奖机会.活动规则如下:一只盒子里装有大小相同的6个小球,其中3个白球,2个红球,1个黑球,抽奖时从中一次摸出3个小球,若所得的小球同色,则获得一等奖,奖金为300元;若所得的小球颜色互不相同,则获得二等奖,奖金为200元;若所得的小球恰有2个同色,则获得三等奖,奖金为100元.
(1)求小张在这次活动中获得的奖金数![]() 的概率分布及数学期望;
的概率分布及数学期望;
(2)若每个人获奖与否互不影响,求该公司某部门3个人中至少有2个人获二等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司有两种发放薪水的方案:
方案一:底薪1800元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为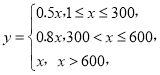
方案二:底薪2000元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为![]()
以下该公司某职工小甲在2019年9月份(30天)送快递的数据,
日送快递单数 | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)从小甲日送快递单数大于15的六天中抽取两天,求这两天他送的快递单数恰好都为16单的概率.
(2)请你利用所学的统计学知识为小甲9月份选择合适的发放薪水的方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com