
【题目】已知函数![]() .
.
(I)讨论函数![]() 的单调性;
的单调性;
(II)若![]() 存在两个极值点
存在两个极值点![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学进入新华书店购买数学课外阅读书籍,经过筛选后,他们都对![]() 三种书籍有购买意向,已知甲同学购买书籍
三种书籍有购买意向,已知甲同学购买书籍![]() 的概率分别为
的概率分别为![]() ,乙同学购买书籍
,乙同学购买书籍![]() 的概率分别为
的概率分别为![]() ,假设甲、乙是否购买
,假设甲、乙是否购买![]() 三种书籍相互独立.
三种书籍相互独立.
(1)求甲同学购买3种书籍的概率;
(2)设甲、乙同学购买2种书籍的人数为![]() ,求
,求![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.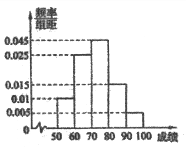
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产![]() 、
、![]() 两种零件,其质量测试按指标划分,指标大于或等于
两种零件,其质量测试按指标划分,指标大于或等于![]() 的为正品,小于
的为正品,小于![]() 的为次品.现随机抽取这两种零件各100个进行检测,检测结果统计如下:
的为次品.现随机抽取这两种零件各100个进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
| 8 | 12 | 40 | 30 | 10 |
| 9 | 16 | 40 | 28 | 7 |
(Ⅰ)试分别估计![]() 、
、![]() 两种零件为正品的概率;
两种零件为正品的概率;
(Ⅱ)生产1个零件![]() ,若是正品则盈利50元,若是次品则亏损10元;生产1个零件
,若是正品则盈利50元,若是次品则亏损10元;生产1个零件![]() ,若是正品则盈利60元,若是次品则亏损15元,在(Ⅰ)的条件下:
,若是正品则盈利60元,若是次品则亏损15元,在(Ⅰ)的条件下:
(i)设![]() 为生产1个零件
为生产1个零件![]() 和一个零件
和一个零件![]() 所得的总利润,求
所得的总利润,求![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)求生产5个零件![]() 所得利润不少于160元的概率.
所得利润不少于160元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com