
【题目】甲乙两名同学参加定点投篮测试,已知两人投中的概率分别是![]() 和
和![]() ,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.
,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.
(Ⅰ)若每人投球3次(必须投完),投中2次或2次以上,记为达标,求甲达标的概率;
(Ⅱ)若每人有4次投球机会,如果连续两次投中,则记为达标.达标或能断定不达标,则终止投篮.记乙本次测试投球的次数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的图象过点A(0,
的图象过点A(0, ![]() ),B(3,3)
),B(3,3)
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(2,+∞)上的单调性,并用单调性的定义加以证明;
(3)若m,n∈(2,+∞)且函数f(x)在[m,n]上的值域为[1,3],求m+n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义域为R的函数 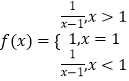 ,若关于x的方程f2(x)+bf(x)+c=0有三个不同的解x1 , x2 , x3 , 则
,若关于x的方程f2(x)+bf(x)+c=0有三个不同的解x1 , x2 , x3 , 则 ![]() 的值是( )
的值是( )
A.1
B.3
C.5
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
, ![]() ,…,
,…, ![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
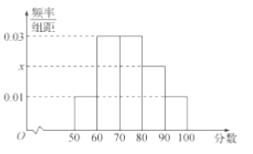
(1)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若在样本中,利用分层抽样的方法从成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求![]() 两组中至少有1人被抽到的概率.
两组中至少有1人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商品在近30天内每件的销售价格P(元)与时间t(天)的函数关系p= ![]()
该商品的日销售量Q(件)时间t(天)的函数关系Q=﹣t+40(0<t≤30,t∈N*)
求该商品的日销售额的最大值,并指出日销售额最大一天是30天中的第几天?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=4x,且f(0)=1.
(1)求二次函数f(x)的解析式.
(2)求函数g(x)=( ![]() )f(x)的单调增区间和值域.
)f(x)的单调增区间和值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com