
【题目】湖南省会城市长沙又称星城,是楚文明和湖湘文化的发源地,是国家首批历史文化名城.城内既有岳麓山、橘子洲等人文景观,又有岳麓书院、马王堆汉墓等名胜古迹,每年都有大量游客来长沙参观旅游.为合理配置旅游资源,管理部门对首次来岳麓山景区游览的游客进行了问卷调查,据统计,其中![]() 的人计划只游览岳麓山,另外
的人计划只游览岳麓山,另外![]() 的人计划既游览岳麓山又参观马王堆.每位游客若只游览岳麓山,则记1分;若既游览岳麓山又参观马王堆,则记2分.假设每位首次来岳麓山景区游览的游客计划是否参观马王堆相互独立,视频率为概率.
的人计划既游览岳麓山又参观马王堆.每位游客若只游览岳麓山,则记1分;若既游览岳麓山又参观马王堆,则记2分.假设每位首次来岳麓山景区游览的游客计划是否参观马王堆相互独立,视频率为概率.
(1)从游客中随机抽取3人,记这3人的合计得分为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)从游客中随机抽取![]() 人(
人(![]() ),记这
),记这![]() 人的合计得分恰为
人的合计得分恰为![]() 分的概率为
分的概率为![]() ,求
,求![]() ;
;
(3)从游客中随机抽取若干人,记这些人的合计得分恰为![]() 分的概率为
分的概率为![]() ,随着抽取人数的无限增加,
,随着抽取人数的无限增加,![]() 是否趋近于某个常数?若是,求出这个常数;若不是,说明理由.
是否趋近于某个常数?若是,求出这个常数;若不是,说明理由.
【答案】(1)分布列见解析,![]() ;(2)
;(2)![]() ;(3)是常数
;(3)是常数![]()
【解析】
(1)据题意,每位游客计划不参观马王堆的概率为![]() ,参加马王堆的概率为
,参加马王堆的概率为![]() ,
,![]() 的可能取值为3,4,5,6,分别求出相应的概率,由此能求出
的可能取值为3,4,5,6,分别求出相应的概率,由此能求出![]() 的分布列和
的分布列和![]() .
.
(2)这![]() 人的合计得分为
人的合计得分为![]() 分,则其中只有1人计划参观马王堆,从而
分,则其中只有1人计划参观马王堆,从而![]() ,设
,设![]() ,利用错位相减法能求出
,利用错位相减法能求出![]() .
.
(3)在随机抽取的若干人的合计得分为![]() 分的基础上再抽取1人,则这些人的合计得分可能为
分的基础上再抽取1人,则这些人的合计得分可能为![]() 分或
分或![]() 分,记“合计得
分,记“合计得![]() 分“为事件
分“为事件![]() ,“合计得
,“合计得![]() 分”为事件
分”为事件![]() ,
,![]() 与
与![]() 是对立事件,推导出
是对立事件,推导出![]() ,由此能求出随着抽取人数的无限增加,
,由此能求出随着抽取人数的无限增加,![]() 趋近于常数
趋近于常数![]() .
.
解:(1)据题意,每位游客计划不参观马王堆的概率为![]() ,记1分;参观马王堆的概率为
,记1分;参观马王堆的概率为![]() ,记2分,则
,记2分,则![]() 的可能取值为3,4,5,6.
的可能取值为3,4,5,6.
其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() 的分布列为
的分布列为
| 3 | 4 | 5 | 6 |
|
|
|
|
|
![]() .
.
(2)因为这![]() 人的合计得分为
人的合计得分为![]() 分,则其中有且只有1人计划参观马王堆,
分,则其中有且只有1人计划参观马王堆,
所以![]() .
.
设![]() ,则
,则![]() .
.
两式相减,得![]()
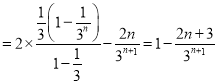 ,
,
所以![]() .
.
(3)在随机抽取若干人的合计得分为![]() 分的基础上再抽取1人,则这些人的合计得分可能为
分的基础上再抽取1人,则这些人的合计得分可能为![]() 分或
分或![]()
分,记“合计得![]() 分”为事件
分”为事件![]() ,“合计得
,“合计得![]() 分”为事件
分”为事件![]() ,则
,则![]() 与
与![]() 为对立事件.
为对立事件.
因为![]() ,
,![]() ,则
,则![]() (
(![]() ),即
),即![]() (
(![]() ).
).
因为![]() ,则数列
,则数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,所以
的等比数列,所以![]() ,
,
即![]() .
.
因为![]() ,则
,则![]() 时,
时,![]() ,从而
,从而![]() ,
,
所以随着抽取人数的无限增加,![]() 趋近于常数
趋近于常数![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() ,若
,若![]() .
.
⑴ 求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
⑵ 将函数![]() 的图象上各点的横坐标伸长为原来的
的图象上各点的横坐标伸长为原来的![]() 倍(纵坐标不变),再将得到的图象向左平移
倍(纵坐标不变),再将得到的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早、晚读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成下表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为30%,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: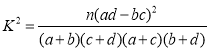 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,离心率为
,离心率为![]() ,点P为椭圆C上一动点,且
,点P为椭圆C上一动点,且![]() 的面积最大值为
的面积最大值为![]() ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)设点![]() ,
,![]() 为椭圆C上的两个动点,当
为椭圆C上的两个动点,当![]() 为多少时,点O到直线MN的距离为定值.
为多少时,点O到直线MN的距离为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com