(本小题满分12分)
已知函数
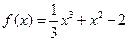
。
(Ⅰ)设{
an}是正数组成的数列,前
n项和为
Sn,其中
a1=3,若点
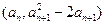
(
n∈N*)在函数
y=
f′(
x)的图象上,求证:点(
n,
Sn)也在
y=
f′(
x)的图象上;
(Ⅱ)求函数
f(
x)在区间(
a-1,
a)内的极值。
(Ⅰ)证明见解析。
(Ⅱ)当
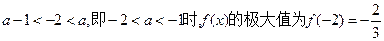
,此时
无极小值;
当
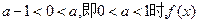
的极小值为
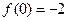
,此时
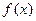
无极大值;
当
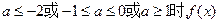
既无极大值又无极小值。
(Ⅰ)证明:因为
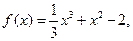
所以
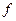
′(
x)=
x2+2
x,
由点
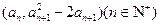
在函数
y=
f′(
x)的图象上,
又
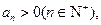
所以
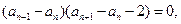
所以
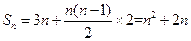
,又因为
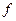
′(
n)=
n2+2
n,所以
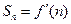
,
故点
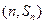
也在函数
y=f′(
x)的图象上.
(Ⅱ)解:
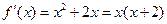
,
由
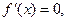
得
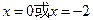
.
当
x变化时,
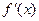
﹑
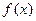
的变化情况如下表:
x
| (-∞,-2)
| -2
| (-2,0)
| 0
| (0,+∞)
|
f′(x)
| +
| 0
| -
| 0
| +
|
f(x)
| ↗
| 极大值
| ↘
| 极小值
| ↗
|
注意到
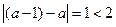
,从而
①当
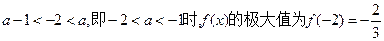
,此时
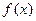
无极小值;
②当
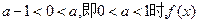
的极小值为
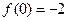
,此时
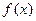
无极大值;
③当
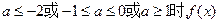
既无极大值又无极小值。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
(文)已知函数
f(
x)的导数为
f′(
x),若
f′(
x)<0(
a <
x <
b)且
f(
b)>0,则在(
a,
b)内必有( )
| A.f(x)=0 | B.f(x)>0 | C.f(x)<0 | D.不能确定 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
曲线y=x
3-3x
2+1在点(1,-1)处的切线方程为( )
| A.y=3x-4 | B.y=-3x+2 | C.y=-4x+3 | D.y=4x-5 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
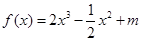
(
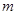
为常数)图象上
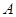
处的切线与直线
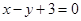
的夹角为45°,则点
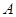
的横坐标为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
在某种工业品的生产过程中,每日次品数
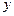
与每日产量
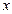
的函数关系式为
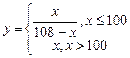
,该工厂售出一件正品可获利
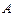
元,但生产一件次品就损失
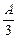
元,为了获得最大利润,日产量应定为多少?
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题6分)已知函数

。
(1)求在
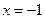
处的切线方程;
(2)求该切线与坐标轴所围成的三角形面积。
查看答案和解析>>

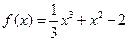 。
。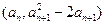 (n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上; 与每日产量
与每日产量 的函数关系式为
的函数关系式为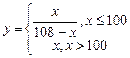 ,该工厂售出一件正品可获利
,该工厂售出一件正品可获利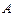 元,但生产一件次品就损失
元,但生产一件次品就损失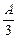 元,为了获得最大利润,日产量应定为多少?
元,为了获得最大利润,日产量应定为多少?