
【题目】已知圆C:(x﹣2)2+(y﹣3)2=16及直线l:(m+2)x+(3m+1)y=15m+10(m∈R).
(1)证明:不论m取什么实数,直线l与圆C恒相交;
(2)求直线l被圆C截得的弦长的最短长度及此时的直线方程.
【答案】(1)证明见解析;(2)最短长度为![]() ,此时直线方程为x+y=7..
,此时直线方程为x+y=7..
【解析】
(1)根据题意,利用直线系求出直线l恒过的定点(3,4),判断该定点在圆的内部,分析即可得答案,
(2)利用圆的半径弦心距与半弦长的关系判断所求直线的位置,求出斜率,即可得到直线方程.
(1)证明:直线l可化为2x+y﹣10+m(x+3y﹣15)=0,
![]() ,解可得
,解可得![]() ,
,
则直线l:(m+2)x+(3m+1)y=15m+10恒过点(3,4).
又有(3﹣2)2+(4﹣3)2=2<16,
则点(3,4)在圆内部,
故不论m为何实数,直线l与圆恒相交;
(2)根据题意,设直线与圆的交点为A、B,M(3,4),
由(1)的结论和直线l过定点M(3,4)且与过此点的圆C的半径垂直时,l被圆所截的弦长|AB|最短,
此时圆心到直线的距离为![]() ,
,
所以![]() ,即最短弦长为
,即最短弦长为![]() .
.
又KCM=![]() =1,则直线l的斜率k=﹣1,
=1,则直线l的斜率k=﹣1,
则直线l的方程为y﹣4=﹣(x﹣3),即x+y=7.


科目:高中数学 来源: 题型:
【题目】命题p:α∈R,sin(π﹣α)=cosα;命题q:“0<a<4”是“关于x的不等式ax2+ax+1>0的解集是实数集R”的充分必要条件,则下面结论正确的是( )
A.p是假命题
B.q是真命题
C.“p∧q”是假命题
D.“p∨q”是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】去年“十一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后,得到如图的频率分布直方图.
后,得到如图的频率分布直方图.

(I)调查公司在抽样时用到的是哪种抽样方法?
(II)求这40辆小型汽车车速的众数和中位数的估计值;
(III)若从这40辆车速在![]() 的小型汽车中任意抽取2辆,求抽出的2辆车车速都在
的小型汽车中任意抽取2辆,求抽出的2辆车车速都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知3acosA=ccosB+bcosC.
(1)求cosA,sinA的值;
(2)若cosB+cosC= ![]() ,求cosC+
,求cosC+ ![]() sinC的值.
sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 ![]() (θ为参数)
(θ为参数)
(1)以原点O为极点,以x轴正半轴为极轴(与直角坐标系xOy取相同的长度单位)建立极坐标系,若点P的极坐标为(4, ![]() ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,利用曲线C的参数方程求Q到直线l的距离的最大值与最小值的差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 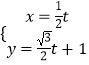 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 ![]() (θ为参数)
(θ为参数)
(1)以原点O为极点,以x轴正半轴为极轴(与直角坐标系xOy取相同的长度单位)建立极坐标系,若点P的极坐标为(4, ![]() ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,利用曲线C的参数方程求Q到直线l的距离的最大值与最小值的差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com