
【题目】在单位正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上运动,给出以下三个命题:
上运动,给出以下三个命题:
①三棱锥![]() 的体积为定值; ②二面角
的体积为定值; ②二面角![]() 的大小为定值;
的大小为定值;
③异面直线![]() 与直线
与直线![]() 所成的角为定值;
所成的角为定值;
其中真命题有( )
A.0个B.1个C.2个D.3个
科目:高中数学 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为10元,被随机分配为1元,2.5元,3元,3.5元,共4份,供甲、乙等4人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于6元的概率是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于不同的直线![]() 与不同的平面
与不同的平面![]() ,有下列六个命题:
,有下列六个命题:
①若![]() 则
则![]() ;
;
②若![]() 则
则![]() ;
;
③若![]() 且
且![]() 则
则![]() ;
;
④若![]() 且
且![]() 则
则![]() ;
;
⑤若![]() 且
且![]() 则
则![]() ;
;
⑥若![]() 且
且![]() 则
则![]() ;
;
其中正确命题的序号是__________;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为2的正方形,平面
是边长为2的正方形,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作直线
作直线![]() ,
,![]() 是直线
是直线![]() 上一动点.
上一动点.
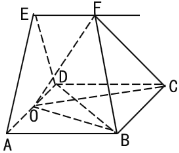
(1)求证:![]() ;
;
(2)若直线![]() 上存在唯一一点
上存在唯一一点![]() 使得直线
使得直线![]() 与平面
与平面![]() 垂直,求此时二面角
垂直,求此时二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com