
【题目】已知函数f(x)是正比例函数,函数g(x)是反比例函数,且f(1)=1,g(1)=2.
(1)求函数f(x)和g(x);
(2)判断函数f(x)+g(x)的奇偶性;
(3)求函数f(x)+g(x)在(0,![]() ]上的最小值.
]上的最小值.
【答案】(1)![]() ;(2)函数f(x)+g(x)是奇函数;(3)
;(2)函数f(x)+g(x)是奇函数;(3)![]()
【解析】本试题主要是考查了函数的奇偶性和函数的解析式以及函数的最值的综合运用。
(1)设f(x)=k1x,g(x)=![]() ,其中k1k2≠0然后结合已知中点的坐标的,饿到结论。
,其中k1k2≠0然后结合已知中点的坐标的,饿到结论。
(2)设h(x)=f(x)+g(x),则h(x)=x+![]() ,
,
∴函数h(x)的定义域是(-∞,0)∪(0,+∞).
∵h(-x)=-x+![]() =-(x+
=-(x+![]() )=-h(x)得到证明。
)=-h(x)得到证明。
(3)由(2)知h(x)=x+![]() ,设x1,x2是(0,
,设x1,x2是(0,![]() ]上的任意两个实数,且x1<x2,,然后运用定义法得到单调性,确定最值。
]上的任意两个实数,且x1<x2,,然后运用定义法得到单调性,确定最值。
解:(1)设f(x)=k1x,g(x)=![]() ,其中k1k2≠0.
,其中k1k2≠0.
∵f(1)=1,g(1)=2,∴k1×1=1,![]() =2.
=2.
∴k1=1,k2=2.∴f(x)=x,g(x)=![]() .
.
(2)设h(x)=f(x)+g(x),则h(x)=x+![]() ,
,
∴函数h(x)的定义域是(-∞,0)∪(0,+∞).
∵h(-x)=-x+![]() =-(x+
=-(x+![]() )=-h(x),
)=-h(x),
∴函数h(x)是奇函数,即函数f(x)+g(x)是奇函数.
(3)由(2)知h(x)=x+![]() ,设x1,x2是(0,
,设x1,x2是(0,![]() ]上的任意两个实数,且x1<x2,
]上的任意两个实数,且x1<x2,
则h(x1)-h(x2)=(x1+![]() )-(x2+
)-(x2+![]() )=(x1-x2)+(
)=(x1-x2)+(![]() -
-![]() )
)
=(x1-x2)(1-![]() )=
)=![]() ,
,
∵x1,x2∈(0,![]() ],且x1<x2,∴x1-x2<0,0<x1x2<2.
],且x1<x2,∴x1-x2<0,0<x1x2<2.
∴x1x2-2<0,(x1-x2)(x1x2-2)>0.
∴h(x1)>h(x2).
∴函数h(x)在(0,![]() ]上是减函数,函数h(x)在(0,
]上是减函数,函数h(x)在(0,![]() ]上的最小值是h(
]上的最小值是h(![]() )=2
)=2![]() .
.
即函数f(x)+g(x)在(0,![]() ]上的最小值是2
]上的最小值是2![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x2-2aln x+(a-2)x,a∈R.
x2-2aln x+(a-2)x,a∈R.
(1)当a=1时,求函数f(x)的图象在点(1,f(1))处的切线方程.
(2)是否存在实数a,对任意的x1,x2∈(0,+∞)且x1≠x2有![]() >a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
>a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》规定,公民全月工资所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额,此项税款按下表分段累计计算:

(1)某人10月份应交此项税款为350元,则他10月份的工资收入是多少?
(2)假设某人的月收入为![]() 元,
元, ![]() ,记他应纳税为
,记他应纳税为![]() 元,求
元,求![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与
轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为![]() ,且各局胜负相互独立,求:
,且各局胜负相互独立,求:
(1)打满3局比赛还未停止的概率;
(2)比赛停止时已打局数ξ的分布列与期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有两个课外活动小组,其中第一小组有足球票6张,排球票4张;第二个小组有
足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,乙从第二小组的10
张票中任抽1张.
(1)两人都抽到足球票的概率是多少?
(2)两人中至少有一人抽到足球票的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在![]() 的人数为12人.
的人数为12人.
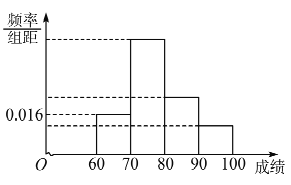
(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌手机销售商今年1,2,3月份的销售量分别是1万部,1.2万部,1.3万部,为估计以后每个月的销售量,以这三个月的销售为依据,用一个函数模拟该品牌手机的销售量y(单位:万部)与月份x之间的关系,现从二次函数![]() 或函数
或函数![]() 中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件.
中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时, ![]() ;
;
(1)求函数![]() 在
在![]() 上的解析式并画出函数
上的解析式并画出函数![]() 的图象(不要求列表描点,只要求画出草图)
的图象(不要求列表描点,只要求画出草图)
(2)(ⅰ)写出函数![]() 的单调递增区间;
的单调递增区间;
(ⅱ)若方程![]() 在
在![]() 上有两个不同的实数根,求实数
上有两个不同的实数根,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com