
 如图,相距14km的两个居民小区M和N位于河岸l(直线)的同侧,M和N距离河岸分别为10km和8km.现要在河的小区一侧选一地点P,在P处建一个生活污水处理站,从P排直线水管PM,PN分别到两个小区和垂直于河岸的水管PQ,使小区污水经处理后排入河道.设PQ段长为t km(0<t<8).
如图,相距14km的两个居民小区M和N位于河岸l(直线)的同侧,M和N距离河岸分别为10km和8km.现要在河的小区一侧选一地点P,在P处建一个生活污水处理站,从P排直线水管PM,PN分别到两个小区和垂直于河岸的水管PQ,使小区污水经处理后排入河道.设PQ段长为t km(0<t<8).分析 (1)如图,以河岸l所在直线为x轴,以过M垂直于l的直线为y轴建立坐标系,设P(s,t),过P作平行于x轴的直线m,作N关于m的对称点N′,则N′(8$\sqrt{3}$,2t-8),PM+PN=PM+PN′≥MN′,可得结论;
(2)由(1)知L=PM+PN+PQ≥t+2$\sqrt{{t}^{2}-18t+129}$(0<t<8),(L-t)2=4(t2-18t+129)在t∈(0,8)上有解,即3t2+(2L-72)t+(516-L2)=0在t∈(0,8)上有解,从而可得处理站P的位置,使所排三段水管的总长最小,并求出此时污水处理站分别到两小区水管的长度.
解答 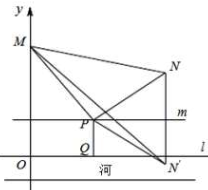 解:(1)如图,以河岸l所在直线为x轴,以过M垂直于l的直线为y轴建立坐标系,则可得M(0,10),N(8$\sqrt{3}$,8),
解:(1)如图,以河岸l所在直线为x轴,以过M垂直于l的直线为y轴建立坐标系,则可得M(0,10),N(8$\sqrt{3}$,8),
设P(s,t),过P作平行于x轴的直线m,作N关于m的对称点N′,则N′(8$\sqrt{3}$,2t-8),
∴PM+PN=PM+PN′≥MN′=2$\sqrt{{t}^{2}-18t+129}$(0<t<8);
(2)设三段水管的总长为L,则由(1)知L=PM+PN+PQ≥t+2$\sqrt{{t}^{2}-18t+129}$(0<t<8);
∴(L-t)2=4(t2-18t+129)在t∈(0,8)上有解,
即3t2+(2L-72)t+(516-L2)=0在t∈(0,8)上有解,
△=(2L-72)2-12(516-L2)≥0,即L2-18L-63≥0
∴L≥21或L≤-3,
∴L的最小值为21,此时对应的t=5∈(0,8),
故N′(8$\sqrt{3}$,2),MN′的方程为y=10-$\frac{\sqrt{3}}{3}$x,
令y=5得x=5$\sqrt{3}$,即P(5$\sqrt{3}$,5),
∴PM=$\sqrt{(5\sqrt{3})^{2}+(5-10)^{2}}$=10,PN=$\sqrt{(5\sqrt{3}-8\sqrt{3})^{2}+(5-8)^{2}}$=6,
∴满足题意的P点距河岸5km,距小区M到河岸的垂线5$\sqrt{3}$km,此时污水处理站到小区M,N的水管长度分别为10km和6km.
点评 本题考查利用数学知识解决实际问题,考查学生解不等式的能力,正确建立关系式是关键.


科目:高中数学 来源: 题型:选择题
| A. | $-39-20\sqrt{5}$ | B. | 0 | C. | 1 | D. | -39 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=1,g(x)=$\frac{x}{x}$ | B. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ | ||
| C. | f(x)=x,g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com